Some observations on the geometry of megakaryocyte mitotic figures: Buckyballs in the bone marrow

To the editor:

In a typical cell, the centrosome replicates at G1-S and then the daughter migrates to the opposite side of the nucleus to help form a biphasic spindle as the cell prepares for division. The position of the centrosomes is critical for ensuring symmetry and segregation of the chromosomes to the progeny.¹  The positioning is also important for cell organization and for asymmetric divisions like in stem cells.²  It is believed that the centrosomes move along a meshwork of microtubules propelled by pushing or pulling with motors from dyneins or kinesins.³  But how they “know” when they have arrived at the correct position is not clear.

Megakaryocytes are giant platelet-producing cells in the marrow that develop through endomitosis, skipping cell divisions and increasing chromosome complement from 2N to 4N to 8N, and so on. The mechanism of this polyploidization is not well understood, but must be extraordinarily complex because for an averaged-sized 32N megakaryocyte almost 750 chromosomes have to be organized onto 16 mitotic plates, tethered to a spindle, and carefully separated during what will be a mitotic cycle with an abortive anaphase and cell division.⁴ 

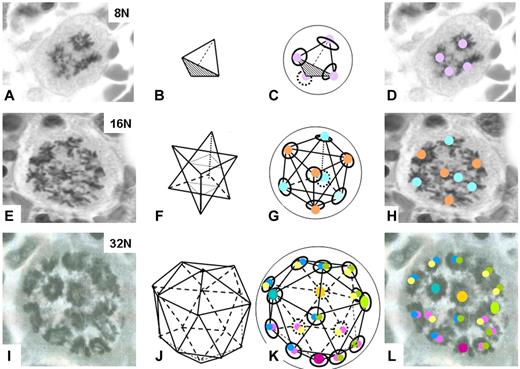
As a Buckminster Fuller enthusiast from the 1970s, I was excited to identify during a bone marrow biopsy examination a 32N megakaryocyte mitosis with almost perfectly organized mitotic plates resembling a geodesic dome (Figure 1I). Given the excitement generated by the discovery of the geodesic C₆₀ molecule,⁵  appropriately named Buckminsterfullerene, and referred to as a Buckyball (appearing on the cover of Science when it was molecule of the year in1991),⁶  I wondered if these megakaryocyte mitoses were Buckyballs in the bone marrow. Could they shed light on the organization of the mitotic apparatus? I attempted to discern the geometry.

Mitotic figures in megakaryocytes are infrequent and those with separated mitotic plates that allow for an examination of geometric relationships are exquisitely rare. Nevertheless, over the years images of 16N mitoses were collected; surprisingly, they did reveal an underlying symmetry. In the 16N images (eg, Figure 1E), the angles of the mitotic plates formed vertices of triangles, the triangles formed tetrahedra, and the entire configuration appeared to form a stella octangular (Figure 1F). This is an unusual geometric composed of 2 tetrahedra one inverted and rotated 180° with respect to the other. Although perplexing, the double tetrahedron for 16N implied a single tetrahedron for 8N, and this was confirmed with examples (Figure 1A-D). In an 8N cell, it seems the 4 centrosomes migrate to positions equidistant from one another as they attempt to orchestrate anaphase. Four equidistant points on a sphere form a tetrahedron.

But what of the stella octangular? It is a fascinating shape with unusual symmetry named by the German mathematician Johannes Kepler in 1611.⁷  It is even believed by some to be a sacred geometry with mystical properties. Although its vertices seem to have no order, in actuality, the vertices form the corners of a cube. So, the 8N mitotic figure forms a tetrahedron, and in the 16N cell the centrosomes appear to localize in the corners of a cube. Eight equidistant points on a sphere form a cube (Figure 1G-H).

If a tetrahedron and cube underlie the organization of the 8N and 16N mitotic apparatus, what geometry is there for 32N? The next perfect geometries are the icosahedron and dodecahedron with 12 and 20 vertices, respectively; hardly what is required to continue the polyploidization to 32N. Sixteen vertices are needed. But what geometry is there for a polygon with 16 vertices?

In yet another cover illustration, but this time on PNAS in 2006, Bulusu et al published the first evidence of a nanostructure for a solid metal.⁸  It was another Buckyball, but this time for a 16-atom gold molecule. The structure was a geodesic with four 6-fold and twelve 5-fold vertices (Figure 1J). Could the configuration of these gold “nanocages,” which parenthetically are having surprising application in medicine,⁹  be the structure of the 32N metaphase? A comparison to the image of the 32N mitosis suggests it is (Figure 1K-L).

The observations noted here illustrate a high order of organization of the mitotic apparatus in polyploid megakaryocytes and may help clarify questions regarding centrosome movement and positioning. It seems the organization may be due to equilibrating forces, likely along microtubules interconnecting the centrosomes. These forces could insure equidistance among the centrosomes and result in a natural symmetry and the ensuing geometry: 4 equidistant points on the sphere, a tetrahedron (8N); 8 equidistant points on a sphere, a cube (16N); and 16 equidistant points on the sphere, a geodesic (32N). Yes, Buckyballs in the bone marrow.