Abstract
Many current experimental results show the necessity of new conceptual approaches to understand hematopoietic stem cell organization. Recently, we proposed a novel theoretical concept and a corresponding quantitative model based on microenvironment-dependent stem cell plasticity. The objective of our present work is to subject this model to an experimental test for the situation of chimeric hematopoiesis. Investigating clonal competition processes in DBA/2-C57BL/6 mouse chimeras, we observed biphasic chimerism development with initially increasing but long-term declining DBA/2 contribution. These experimental results were used to select the parameters of the mathematical model. To validate the model beyond this specific situation, we fixed the obtained parameter configuration to simulate further experimental settings comprising variations of transplanted DBA/2-C57BL/6 proportions, secondary transplantations, and perturbation of stabilized chimeras by cytokine and cytotoxic treatment. We show that the proposed model is able to consistently describe the situation of chimeric hematopoiesis. Our results strongly support the view that the relative growth advantage of strain-specific stem cells is not a fixed cellular property but is sensitively dependent on the actual state of the entire system. We conclude that hematopoietic stem cell organization should be understood as a flexible, self-organized rather than a fixed, preprogrammed process.
Introduction
Many experimental findings on heterogeneity, flexibility, and plasticity of hematopoietic and other tissue stem cells1-6 are currently challenging classical stem cell concepts and clearly show the necessity of novel conceptual approaches to understand tissue stem cell organization.7-13 Recently, we proposed a new theoretical framework of tissue stem cell organization,14 replacing the classical view on tissue stem cells of being preprogrammed entities by a dynamic perspective based on self-organizing principles. Applying these principles to the hematopoietic stem cell system leads to the concept of within-tissue plasticity. This concept and the corresponding quantitative, mathematical model have previously been described in detail.15 Here we briefly summarize the basic assumptions.
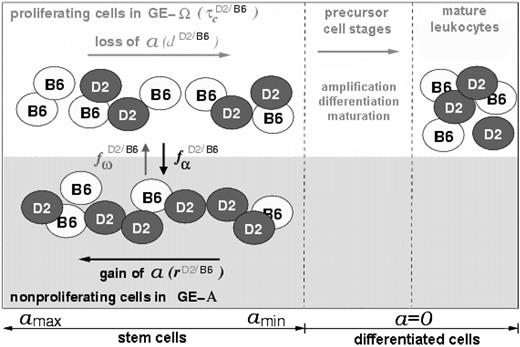
We assume that cellular properties can reversibly change within a range of potential options. The direction of cellular development and the decision as to whether a certain property is actually expressed depends on the internal state of the cell and on signals from its growth environment. Individual cells are considered to reside in 1 of 2 growth environments (GE-A or GE-Ω). The state of each cell is characterized by its actual growth environment, by its position in the cell cycle (G1,S,G2,M,or G0), and by a property (a) that describes its affinity to reside in GE-A. Whereas cells in GE-Ω gradually lose this affinity, cells in GE-A are able to gradually regain it. Furthermore, cells in GE-A are assumed to be nonproliferating (ie, in G0), while cells in GE-Ω are assumed to proliferate with an average generation time τc. The transition of cells between the 2 GEs is modeled as a stochastic process. The corresponding transition intensities (probabilities of growth environment change per time step) depend on the current value of the affinity a and on the number of stem cells residing in GE-A and GE-Ω, respectively. This cell number dependency is described in the model by the transition characteristics fα and fω (Supplemental Figure S1; at the Blood website, see the Supplemental Data link at the top of the online article). If the attachment affinity a of an individual cell has fallen below a certain threshold (amin), this cell is released from the stem cell compartment and starts the formation of a clone of differentiated cells.
Using simulation studies, we have previously shown that this model can describe a large variety of observed phenomena, such as heterogeneity of clonogenic and repopulation potential (demonstrated in different types of colony formation and repopulating assays), fluctuating clonal contribution (observed in chimeric animals or in individual clone-tracking experiments), or changing cell-cycle activity of primitive progenitors (described by the use of different S-phase labeling studies).15,16
The quantitative information contained in experiments on clonal competition and on unstable or fluctuating chimerism of hematopoietic cells17-24 provide an additional, important possibility to test our model and to provide insight into generating and regulating mechanisms of these intriguing phenomena.
To apply our stem cell model to a chimeric situation (Figure 1), we consider 2 populations of cells within 1 model system. These populations potentially differ in their model parameters d, r, τc, fα, or fω. This approach allows the analysis of the influence of these model parameters on the competitive behavior of the 2 cell types and, therefore, on the dynamics of chimerism development.
Schematic representation of the model concept for a chimeric situation. Cellular development within the stem cell compartment (left) is characterized by the possibility of individual cells (black and white circles) to reside in 2 different growth environments (GE-A, gray; GE-Ω, white). The affinity (a) of cells to reside in GE-A can reversibly change depending on the actual GE (gain in GE-A, loss in GE-Ω). The processes of a-loss/gain and of transition between the 2 growth environments (characterized by the model parameters d, r, and fα, fω, respectively) are assumed to be strain specific, illustrated by the D2/B6 superscripts. The same holds for the process of proliferation (amplification due to cell division), which is described by the average generation time τc. Cells that have lost the potential to change to GE-A and, therefore to regain a (denoted as differentiated cells), will pass through different precursor stages to become mature leukocytes. Regulation processes of precursor and mature cell stages are neglected in the current model version.
Schematic representation of the model concept for a chimeric situation. Cellular development within the stem cell compartment (left) is characterized by the possibility of individual cells (black and white circles) to reside in 2 different growth environments (GE-A, gray; GE-Ω, white). The affinity (a) of cells to reside in GE-A can reversibly change depending on the actual GE (gain in GE-A, loss in GE-Ω). The processes of a-loss/gain and of transition between the 2 growth environments (characterized by the model parameters d, r, and fα, fω, respectively) are assumed to be strain specific, illustrated by the D2/B6 superscripts. The same holds for the process of proliferation (amplification due to cell division), which is described by the average generation time τc. Cells that have lost the potential to change to GE-A and, therefore to regain a (denoted as differentiated cells), will pass through different precursor stages to become mature leukocytes. Regulation processes of precursor and mature cell stages are neglected in the current model version.
Preliminary simulation studies, based on the above-described concept, led to 2 major qualitative predictions. First, we predicted that small differences in model parameters may cause unstable chimerism with a slow but systematic long-term trend in favor of one clone. Secondly, we predicted that the chimerism depends on the actual status (ie, cell numbers) of the entire system. Therefore, system perturbations (eg, by stem cell transplantation after myeloablative conditioning or cytokine or cytotoxic treatment) are expected to result in significant changes of chimerism levels within a short period of time.
It was our objective to subject these qualitative predictions to an experimental test and to investigate whether these phenomena could be explained consistently by one single parameter set of the model. The starting point for our experimental design was the observation that the contribution of DBA/2 (D2) cells to peripheral blood production in C57BL/6 (B6) – D2 allophenic mice declines over time but can be reactivated by a bone marrow transplantation into lethally irradiated B6 D2 F1 (BDF1) mice.25 To quantitatively compare experimental data and simulation results, we investigated the chimerism kinetics in primary and secondary B6-D2 radiation chimeras in much greater detail. Beyond this, we performed experiments inducing transient perturbations of chimerism in fully reconstituted animals using cytokine stimulation or cytotoxic treatment.
Materials and methods
Mice
Female B6D2F1OlaHsD (BDF1) and timed pregnant DBA/2OlaHsd (D2) and C57BL/6JolaHsD (B6) mice were purchased from Harlan (Horst, The Netherlands). BDF1 mice were used at the age of 10 to 12 weeks as recipients.
Experimental design
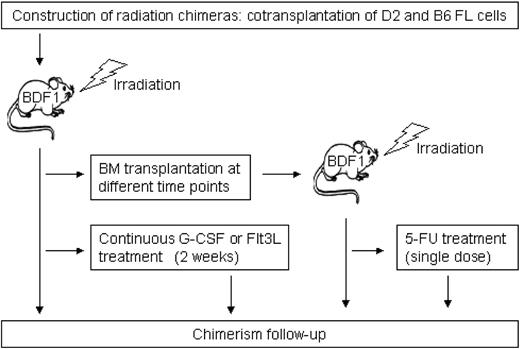
Figure 2 shows a schematic overview of the experimental design. Primary and secondary radiation chimeras were used to analyze the long-term chimerism kinetics. Furthermore, we analyzed perturbations of stable systems by treating primary and secondary radiation chimeras with cytokines (recombinant human granulocyte colony-stimulating factor [rhG-CSF], recombinant human fms-like tyrosine kinase 3 ligand [rhFlt3-ligand]) and cytotoxic agents, respectively.
Production of fetal liver radiation chimeras
Chimeras were constructed as described previously.26 Briefly, fetal livers (FLs) were isolated from timed pregnant B6 and D2 mice (14 days postcoitus). Lethally irradiated (9.5 Gy, 4 hours prior to transplantation) BDF1 mice (n = 40) underwent transplantation with a total of 2 × 106 FL cells. We used FL cells instead of adult bone marrow (BM) cells to avoid graft-versus-graft reactions. There are no alloreactive T cells present in day-14 FL cells. We do not expect any FL-specific effect on long-term chimerism in these chimeras.
D2 and B6 FL cells were transplanted at a ratio of 1:4 because earlier experiments26 revealed that this ratio is best suited to provide equal initial B6 and D2 contributions in the peripheral blood of recipient mice.
Secondary transplantation
We performed secondary transplantation of BM cells from 2 individual chimeric donors at 133 and 588 days after primary transplantation of FL cells. These donors were selected because they showed highly distinct D2/B6 leukocyte ratios in the peripheral blood at the time of transplantation (9:11 in the first and 1:9 in the second donor mouse). A total of 2 × 106 (first donor) and 2.5 × 106 (second donor) unfractionated BM cells were transplanted into cohorts of 5 and 12 lethally irradiated female BDF1 mice.
Determination of peripheral blood cell chimerism
Blood samples (about 50 μL) were drawn from the retro-orbital plexus of each chimera at various time points after transplantation. Erythrocytes were lysed by hypotonic shock (0.16 M NH4Cl, 1.0 × 10–4 M EDTA [ethylenediaminetetraacetic acid], 0.017 M NaCl, 10 minutes at room temperature). Leukocytes were stained with fluorescein isothiocyanate (FITC)–labeled antimouse H-2Kd and biotin-labeled antimouse H-2Kb (PharMingen, San Diego, CA), which detect D2 and B6 leukocytes, respectively. Cells were washed twice and stained with streptavidin-phycoerythrin (PE) (PharMingen). The percentage of leukocytes derived from D2, B6, and BDF1 was assessed by flow cytometry (FACSCalibur, Becton Dickinson, Palo Alto, CA).26 To avoid repetitive bleeding, not all mice were analyzed at every time point.
Cytokine treatment using rhG-CSF and Flt3-ligand
Ten months after FL transplantation, 2 cohorts of 4 primary recipients were treated for 14 days with either rhG-CSF (a gift from Amgen, Thousand Oaks, CA) or rhFlt3-ligand (a gift from Immunex, Seattle, WA) using ALZET mini-osmotic pumps (DURECT, Cupertino, CA). Administered doses were 2.5 μg rhG-CSF per mouse per day (n = 4) and 5 μg Flt3-ligand per mouse per day (n = 4).
Cytotoxic treatment using 5-fluorouracil (5-FU)
A group of 4 chimeric mice that underwent secondary transplantation received 150 mg/kg 5-FU (Pharmachemie, Haarlem, The Netherlands) to deplete the progenitor pool. The 5-FU was appropriately diluted in 150 μL phosphate-buffered saline (PBS) and administered intraperitoneally in a single injection.
Cobblestone area–forming cell assay
The number of transplanted stem cells was estimated using the cobblestone area–forming cell assay (CAFC).27
Statistical analysis
To statistically test the significance of experimentally observed temporal trends in chimerism development we applied a linear mixed-effects model,28 which allows us to consider the correlation structure of repeated measurements within individuals. Changes of mean chimerism levels at 2 individual time points were tested using classical t-tests. Statistics and graphics have been produced using the statistical computing environment R.29
Simulation procedure
To simulate the chimeric development of individual mice, the actual status of each stem cell, characterized by its attachment affinity (a), its position in the cell cycle (c), and its current growth environment (GE-A, GE-Ω, or pool of differentiated cells), is updated at discrete time steps of 1 hour (for details, see Roeder and Loeffler15 ). Additionally, the actual number of stem cells in GE-A and GE-Ω and of differentiated cells is recorded at these time points. To determine the number of peripheral blood leukocytes in the simulations, the pool of mature cells (Figure 1) is used. Hereby it is assumed that the number of mature leukocytes is proportional to the number of cells released from the stem cell compartment. Details of amplification, differentiation, and maturation within precursor cell stages are neglected in the current model version. The maturation time for precursor cells, including the lifetime of mature peripheral blood leukocytes, has been preset for all model cells to 5 days for reconstituting and 10 days for stabilized systems.30 Chimerism levels are obtained by calculating the D2 proportion among model cells within the mature leukocyte compartment.
Due to the stochastic nature of the growth environment transition of stem cells, individual simulation runs produce different chimerism levels even though identical parameter sets are used. Therefore, to determine the mean chimerism levels under a specific parameter set, repeated simulation runs (n = 100) have been performed. To illustrate the average behavior and the variability of individual simulations, the mean and the standard deviation (SD) of chimerism levels are determined at each time step.
Starting from a parameter configuration that has previously been demonstrated to consistently explain a variety of experimental phenomena in the nonchimeric situation,15 we fitted the simulation outcome to the observed chimerism development in primary irradiation chimeras initiated with a 1:4 ratio of transplanted D2 and B6 FL cells. The fitting process has been realized by varying the initial D2 proportion of stem cell and the shape parameters of the transition characteristics fαD2 and fωD2 according to an evolutionary strategy31 (see “Parameter estimation according to an evolutionary strategy”).
To evaluate the proposed model for the situation of competitive hematopoiesis, this parameter set has been applied to further experimental settings and the resulting simulation results have been compared with experimental data. To illustrate the goodness of fit, we use graphical representations and, if applicable (availability of experimental raw data), the average (over all time points) proportion of measurements within the mean ± 1 standard deviation (SD) interval of the simulation denoted by Δ.
Parameter estimation according to an evolutionary strategy
In the “first generation,” the average chimerism development of 20 individual simulation runs for an initial parameter configuration is determined and the sum of squared residuals
is calculated as a fitness measure. Herein,
Specific model assumptions
Construction of chimeras and long-term chimerism follow-up. To simulate the development of radiation chimeras, model systems are initiated by 2 cell populations that differ in their cellular parameters τc, fα, and fω. Different compositions of transplants with respect to strain ratio or quality of progenitors are realized by varying the D2 proportion (ranging from 10% to 90%) and the starting a values (ranging from 0.01 to 1) of the initiating model cells. Primary model chimeras were initiated with a low D2 proportion in the range of 10% to 30%, with a values uniformly distributed on the interval [0.01; 1]. The total number of engrafting stem cells was set to 20 (which equals about 6% of the model steady state numbers), motivated by an estimate of 1 stem cell in 105 BM cells.32 Residual F1 cells in the host systems are neglected.
Secondary transplantation and follow-up of reconstitution kinetics. Secondary transplantations are simulated by the initiation of empty model systems (representing lethally irradiated BDF1 hosts), with 20 model cells randomly sampled from the stem cell pool of a previously simulated primary chimera. This sampling induces an initial D2/B6 ratio and an a distribution comparable to the stem cell population of the donor at the time of transplantation.
Transient perturbations of stable systems (cytokine stimulation and cytotoxic treatment). rhG-CSF and rhFlt3-ligand stimulations are simulated identically by a transient increase of the transition intensity fω, modeling an enhanced activation of stem cells into cycle. To be more specific, for the duration of the treatment the value of the (otherwise stem cell number–dependent) characteristic fω is fixed to a value of 0.5 and 0.7 for B6 and D2, respectively.
The 5-FU effect is simulated by a kill of all model cells entering S phase for 12 hours from the time point of treatment.
Computer implementation
The program is implemented in C++, and simulations have been performed on a LINUX platform.
Results
Chimerism development in unperturbed radiation chimeras
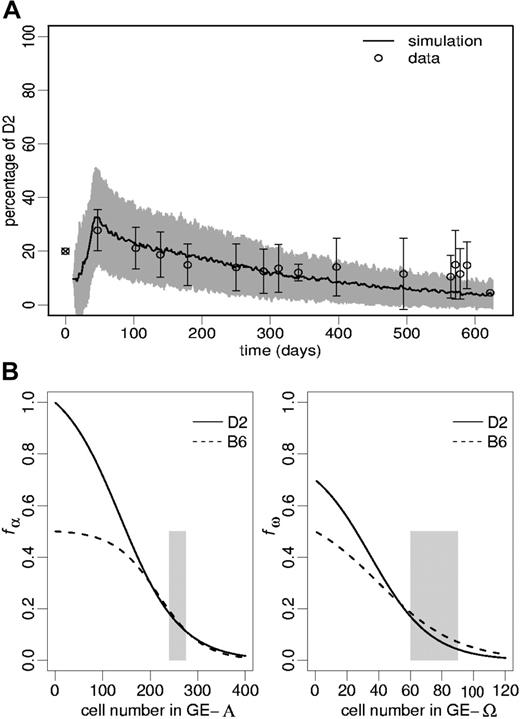
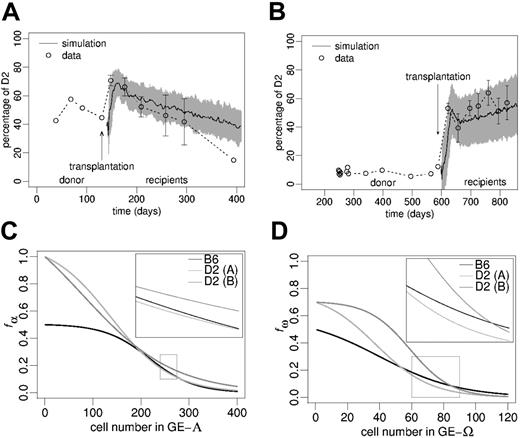
Experimental results. We investigated progression of chimerism in B6-D2 radiation chimeras over a period of up to 20 months. The content of primitive progenitor cells in the FL cell transplants was estimated using a CAFC assay, with CAFC day-35 frequencies (per 105) of 7.3 for D2 and 0.4 for B6. The data points in Figure 3A show the proportions of D2 peripheral blood leukocytes starting from an initial D2/B6 ratio of 1:4 (ie, 20% D2) of transplanted FL cells. The increasing variability of the data toward the end of the measuring period can partially be explained by the fact that early chimerism values (before day 300) have been obtained from a consistent set of 16 mice. In contrast, at later time points some of these mice had been used for other experiments, and chimerism measurements from (identically constructed) chimeras that had not been tracked within the first 300 days after construction were included into the analysis. One recognizes that after a maximum of about day 40 after transplantation there is a time-dependent decline of D2 contribution. Accounting for the inhomogeneity of the data set at late time points, we tested the D2 decline within the period of day 40 to 290 and show that it is statistically significant (P < .001).
Chimerism development in unperturbed radiation chimeras. (A) The open circles represent the observed chimerism levels (mean ± 1 SD) in primary radiation chimeras. The ⊗ illustrates the D2/B6 ratio in the FL cell transplant. The simulated chimerism of mature model leukocytes is given by an average of 100 simulation runs (solid line) and its corresponding SD (gray shade). The goodness of fit measure, Δ, equals 0.80. The used transition intensities fα and fω (obtained by fitting the model to the data points) are shown in panels B and C, respectively. The shaded areas in panels B and C indicate stem cell numbers consistent with a regenerated stabilized model system.
Chimerism development in unperturbed radiation chimeras. (A) The open circles represent the observed chimerism levels (mean ± 1 SD) in primary radiation chimeras. The ⊗ illustrates the D2/B6 ratio in the FL cell transplant. The simulated chimerism of mature model leukocytes is given by an average of 100 simulation runs (solid line) and its corresponding SD (gray shade). The goodness of fit measure, Δ, equals 0.80. The used transition intensities fα and fω (obtained by fitting the model to the data points) are shown in panels B and C, respectively. The shaded areas in panels B and C indicate stem cell numbers consistent with a regenerated stabilized model system.
Model results. Because an identical parameter choice for both strains would always result in a constant chimerism, an explanation of the observed systematic biphasic changes in chimerism levels is inevitably requiring some difference in the model parameters. Due to the documented difference between D2 and B6 cells with respect to their cycling activity,26 we assumed different average generation times (
However, solely assuming this difference is not sufficient to explain the observed chimerism development. Therefore, we performed a sensitivity analysis of the model parameters controlling the cellular development (ie, the differentiation coefficient d, the regeneration coefficient r, and the transition characteristics fα and fω). This means, starting from the previously established parameter configuration,15 including the experimentally motivated difference in the cycling activity, we varied one parameter after another (keeping all other parameters fixed) to investigate its effect on temporal chimerism development. We found that only differences in the transition characteristics induce the observed biphasic pattern.
The simulation presented in Figure 3A used characteristics fαD2 and fωD2 as shown in Figure 3B-C. These had been selected by fitting the simulations to the data set according to an evolutionary strategy. Because the D2/B6 ratio of initially engrafting stem cells cannot exactly be determined experimentally, we furthermore allowed a restricted variation (± 10% with respect to the ratio of transplanted FL cells) of this ratio in the fitting procedure, resulting in a predicted D2 engraftment of 10% immediately after transplantation.
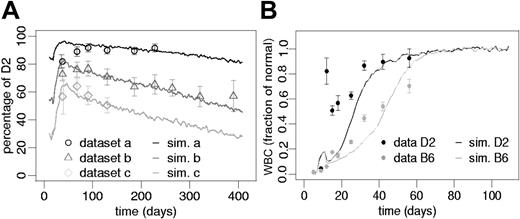
Our simulations demonstrate that variations in the initial D2/B6 ratio (30%, 50%, and 85%), without any further change of the model parameters, are sufficient to explain the experimentally observed heterogeneity of chimerism development in different experiments (Figure 4A).
Simulation results on strain differences. (A) Effect of the initial D2/B6 ratio. Data points represent the results (mean ± 1 SD) from 3 independent experiments. Data sets a and b used initially transplanted D2 proportions of 80% and 50% FL cells. Data set c (previously published26) used an initial D2 proportion of 20%. However, a different irradiation scheme as in the current study was used in this case. Solid lines represent corresponding average simulation results using identical parameter sets but different initial D2 proportions: a, 85%, b, 50%, and c, 30%. Goodness of fit measures, Δ, are as follows: a, 0.78; b, 0.89; and c, 0.92. (B) Reconstitution in nonchimeric situations. Black (D2) and gray (B6) dots represent mean leukocyte numbers (± 1 SEM) normalized to steady state counts of 6.7 × 106for D2 and 7.4 × 106for B6 mice (previously published33). The solid lines (black, D2; gray, B6) show average simulation results of reconstituting nonchimeric model systems starting from 20 initiating stem cells. Given is the fraction of normal steady state white blood cells in the mature leukocyte compartment of the simulation model using the D2 and the B6 parameter sets, respectively.
Simulation results on strain differences. (A) Effect of the initial D2/B6 ratio. Data points represent the results (mean ± 1 SD) from 3 independent experiments. Data sets a and b used initially transplanted D2 proportions of 80% and 50% FL cells. Data set c (previously published26) used an initial D2 proportion of 20%. However, a different irradiation scheme as in the current study was used in this case. Solid lines represent corresponding average simulation results using identical parameter sets but different initial D2 proportions: a, 85%, b, 50%, and c, 30%. Goodness of fit measures, Δ, are as follows: a, 0.78; b, 0.89; and c, 0.92. (B) Reconstitution in nonchimeric situations. Black (D2) and gray (B6) dots represent mean leukocyte numbers (± 1 SEM) normalized to steady state counts of 6.7 × 106for D2 and 7.4 × 106for B6 mice (previously published33). The solid lines (black, D2; gray, B6) show average simulation results of reconstituting nonchimeric model systems starting from 20 initiating stem cells. Given is the fraction of normal steady state white blood cells in the mature leukocyte compartment of the simulation model using the D2 and the B6 parameter sets, respectively.
Furthermore, we tested this parameter configuration (obtained for the competition situation in chimeric systems) for the reconstituting behavior of nonchimeric systems. Figure 4B shows that both parameter sets (D2, B6) are able to generate stable nonchimeric systems after system initiation with a low number of D2 or B6 cells, respectively. Herein, the model predicts a faster reconstitution of D2 compared with B6 systems, which is consistent with previously published observations.33
Reactivation of clone activity after retransplantation and long-term chimerism in secondary chimeras
Experimental results. Transplantation of bone marrow cells from 2 primary radiation chimeras at day 133 and 588 after first transplantation (2 different experiments), into secondary cohorts of lethally irradiated BDF1 mice clearly showed a reactivation of D2 contribution in the peripheral blood (Figure 5A-B). In both experiments we found significantly increased D2 contributions (P < .001 in both cases) immediately after transplantation compared with the chimerism level in the donor animals prior to transplantation. However, regarding the long-term behavior, we noted remarkable differences between the 2 experiments. Whereas the D2 contribution within the animals of one experimental cohort showed a statistically significant (P = .0015) decline (Figure 5A), an increase in the D2 contribution could be demonstrated (P = .012) in the second cohort (Figure 5B).
Chimerism development in secondary hosts after BM transplantation.(A-B) The circles show the experimentally observed peripheral blood leukocyte chimerism in 2 individual primary radiation chimeras (single values) and in corresponding cohorts of secondary host mice (mean ± SD). The solid lines show average simulations (gray shade: simulation SD) for the chimerism development in the secondary chimeras (goodness of fit measures, Δ: (A) 0.56, (B) 0.80). The simulation scenarios in panels A and B differ with respect to transition characteristics (C-D) and the initiating D2/B6 ratio according to the experimental situation. (C-D) Transition characteristics used to generate the simulations in panels A and B, respectively. The zoomed regions represent the regulatory windows responsible for long-term chimerism development in fully reconstituted systems.
Chimerism development in secondary hosts after BM transplantation.(A-B) The circles show the experimentally observed peripheral blood leukocyte chimerism in 2 individual primary radiation chimeras (single values) and in corresponding cohorts of secondary host mice (mean ± SD). The solid lines show average simulations (gray shade: simulation SD) for the chimerism development in the secondary chimeras (goodness of fit measures, Δ: (A) 0.56, (B) 0.80). The simulation scenarios in panels A and B differ with respect to transition characteristics (C-D) and the initiating D2/B6 ratio according to the experimental situation. (C-D) Transition characteristics used to generate the simulations in panels A and B, respectively. The zoomed regions represent the regulatory windows responsible for long-term chimerism development in fully reconstituted systems.
Model results. Without changing the parameter configuration previously obtained (Figure 3A), the simulations predict that a reduction of the total stem cell pool size, as assumed for the transplantation setting, induces an initial elevation of the D2 contribution in the host (compared with donor chimerism prior to transplantation) followed by a gradual D2 decline (Figure 5A).
However, to explain the chimerism development observed in the second experimental cohort (Figure 5B) it was necessary to adjust the parameter configuration. Again, we used an evolutionary strategy to select suitable transition characteristics fα and fω. The initial D2 proportion was set to 12%, according to the donor chimerism at the time of transplantation. The results of the parameter fitting revealed that small quantitative variations of fα and fω (Figure 5C-D) are sufficient to explain the observed chimerism development (Figure 5B). Further examples, illustrating the sensitive influence of minor, quantitative changes in the transition characteristics on the qualitative long-term development of chimerism, are given in the supplemental material (Figure S2).
Transient perturbations of stable systems by cytokine or cytotoxic treatment
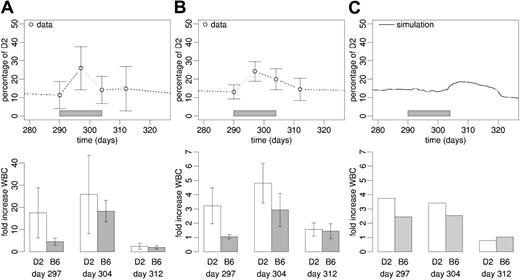
Experimental results. Cytokine stimulation as well as 5-FU treatment induced transient perturbations of the system behavior (Figures 6A-B and 7A). With respect to cytokine stimulation, we observed a significant increase of the D2 leukocyte proportion at day 7 of treatment compared with pretreatment levels using rhFlt3-ligand (P = .008) and rhG-CSF (P = .016). The same is true for the increase in total white blood cell (WBC) numbers using rhFlt3-ligand (P = .042) and rhG-CSF (P < .001). Although the chimerism had widely returned to starting values by the end of treatment (day 304), there was still a statistically significant increase (P = .008 and P = .009) in WBCs compared with the pretreatment situation at this time point (Figures 6A-B).
Cytokine stimulation. Experimental data (mean ± SD) of (A) rhFlt3-ligand and (B) rhG-CSF stimulation of stabilized (day 290 after transplantation) primary radiation chimeras. (C) Corresponding average simulation result of cytokine stimulation (no difference assumed for rhFlt-3-ligand and rhG-CSF effects). In all panels, the upper graphics show the chimerism development, with gray bars representing the period of cytokine stimulation. The lower graphics show white blood cell counts at day 7, 14, and 21 after the start of treatment, relative to pretreatment levels.
Cytokine stimulation. Experimental data (mean ± SD) of (A) rhFlt3-ligand and (B) rhG-CSF stimulation of stabilized (day 290 after transplantation) primary radiation chimeras. (C) Corresponding average simulation result of cytokine stimulation (no difference assumed for rhFlt-3-ligand and rhG-CSF effects). In all panels, the upper graphics show the chimerism development, with gray bars representing the period of cytokine stimulation. The lower graphics show white blood cell counts at day 7, 14, and 21 after the start of treatment, relative to pretreatment levels.
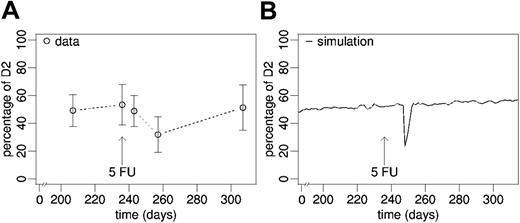
Cytotoxic treatment. (A) Experimental data (mean ± SD) and (B) average simulation on chimerism development after disturbance of stabilized secondary chimeras (day 239 after bone marrow transplantation) by a single dose of 5-FU.
Cytotoxic treatment. (A) Experimental data (mean ± SD) and (B) average simulation on chimerism development after disturbance of stabilized secondary chimeras (day 239 after bone marrow transplantation) by a single dose of 5-FU.
The treatment of fully reconstituted mouse chimeras with a single dose of 5-FU appeared to induce a delayed drop of the D2 contribution to peripheral blood leukocytes (Figure 7A). The nadir of D2 chimerism (day 257), however, was not significantly different from pretreatment values (P = .100), which might be due to the low number of post-treatment data points (n = 3). The measurement at 70 days after treatment revealed that the effect was transient and chimerism returned to pretreatment levels.
Model results. To test the system response to dynamic perturbation during stable chimerism, we modeled the effect of cytokines (rhG-CSF or rhFlt3-ligand), which we assumed to destabilize the balance between the 2 model growth environments due to their cell activation and migration-inducing capacity, by fixing the transition characteristic fω (describing the activation of stem cells into cycle) at high level (Supplemental Table S1). Despite the change in fω,no further parameters were changed with respect to the configuration obtained by the fit to the data in Figure 3A. In this setting the model predicts a delayed skewing of chimerism toward the D2 cell type and a minor but strain-specific increase in the numbers of mature model cells (Figure 6C). The simulated cytokine effect is only transient, and the system returns to pretreatment levels within about 20 days.
Furthermore, we modeled the effect of reducing the actively cycling stem cell pool size using the S phase–specific cytotoxic drug 5-FU. Again, we used the parameter configuration estimated for the primary chimeras. The simulations predict a declining D2 contribution (Figure 7A). Similar to the effect of cytokine stimulation, the cytotoxic treatment results in a transient effect on chimerism only.
Discussion
This work provides an experimental test of our novel concept of tissue stem cell organization based on the within-tissue plasticity idea for the situation of competitive hematopoiesis. Using a parameter configuration obtained by fitting the model to one specific data set, the mathematical model made several predictions for the situation of clonal competition and unstable chimerism. We demonstrated that this single-parameter configuration can explain most of the presented phenomena in the chimeric situations and is also consistent with the variety of further phenomena previously analyzed.15 Notably, parameter adjustments for the simulation of each individual data set would provide even better model fits. However, it was our main goal to validate the model by the application of one parameter configuration to several independent data sets.
Our results suggest that chimerism levels, observed in the peripheral blood, depend on the actual dynamic status of the stem cell system. We show that alterations of total stem cell pool size, selective reductions of stem cell subpopulations, and cytokine stimulation influence the competitive behavior of chimeric hematopoiesis. The simulation studies reveal that variations in strain-specific cellular properties of stem cells, which sensitively affect the competitive behavior in a chimeric situation, do not necessarily influence their growth and repopulating potential in a nonchimeric system. These findings point to the relative nature of stem cells and their repopulating potential in general. For example, a particular stem cell clone that exhibits a competitive growth advantage in a specific situation might behave differently in another dynamic situation or if exposed to a different competitor clone. Therefore, stem cell potential must not be regarded as an isolated cellular property but must be understood as a dynamic property taking into account the individual cellular potential, the cell-cell interactions, and the cell-microenvironment interactions. This has potentially important implications for the treatment of clonal disorders, gene therapeutic strategies, or tissue engineering processes where the aim is to control the competitive potential of a specific cell type or clone.
To explain the specific competitive behavior of D2 and B6 cells in the chimeric situation, different hypotheses have been suggested. One of them is a strain difference in the number of long-term reconstituting stem cells.33,34 However, although a higher number of primitive progenitor cells of one strain type would explain a relative growth advantage in the reconstituting situation, it would not explain the reversion of the competitive behavior in fully reconstituted animals. The same argumentation holds for a fixed, strain-specific difference in cycling activity.26 Another proposed mechanism underlying the time-dependent changes of the competitive behavior of D2 cells is an age-dependent deterioration of long-term repopulating ability, which has been reported to be more pronounced in D2 cells.35,36 An age-dependent, irreversible decline of repopulating potential, however, contrasts the observation that the D2 contribution can be reactivated by transplantation, even in aged mice.
As a key result, the present analysis provides an alternative explanation for the variety of clonal competition patterns observed. The model proposes that strain differences in the stem cell–growth environment interactions, quantified by the transition characteristics fα and fω, are responsible for a wide range of phenomena. Such a process can explain the experimentally observed smooth, longterm changes of the D2 contribution and, due to the dynamic control, also the reactivation of the D2 clone in any setting with a sufficiently high reduction of the stem cell pool size. Furthermore, the model analysis reveals that different patterns of D2 contribution in the regenerating phase (Figure 4A) can be explained consistently within the model paradigm by solely changing the D2/B6 ratio of engrafting stem cells without varying any other parameter. Regarding the long-term behavior of chimerism development, it is remarkable how sensitively the model system reacts to small quantitative differences in the dynamic parameters such as the transition characteristics. The assumption that these characteristics are inheritable (ie, clonal) properties provides an explanation for the heterogeneity of long-term chimerism development in secondary chimeras. Along these lines, the qualitative similarity of chimerism development in donor and host (Figure 5A-B) could be explained by the preferred sampling of transplanted stem cells from dominating clones in the donor. Of note, the introduction of a limited variability in the transition characteristics does not influence the initial growth advantage of D2 cells following transplantation, because the differences of the transition characteristics for low cell numbers are assumed to be large compared with the interclonal variability (compare Figure 5D-E). Concluding from these results, we predict that small inheritable differences of cellular properties (ie, clonal heterogeneity) that do not affect the general repopulating potential of a particular clone are able to explain similarities in the engrafting pattern of clonally derived transplants as reported by Muller-Sieburg et al37,38 (modeling work in progress39 ).
In addition to the present assumption of identical cellular properties within the 2 strain types (no clonal heterogeneity), the current model version contains further simplifications. The molecular processes involved in the dynamic control of stem cell differentiation and proliferation are currently subsumed in the transition characteristics fα and fω, which model complex properties, including cellular and microenvironmental components. Revealing the regulatory mechanisms will include a detailed investigation of underlying molecular processes active in the different cellular states. Here, recent findings by Merchant et al40 suggest that the proliferating and the quiescent cells have a different gene expression profile, which can be switched either way upon perturbation, an observation actually confirming the present model. A related observation was made by Dykstra et al,41 indicating that switching self-renewal programs on or off can take only a few hours. Numerous publications are now available that report that overexpression or silencing of particular genes (eg, of the HOX family, of the signal transducer and activator of transcription pathway, or of cell-cycle regulation) can affect the repopulating potential and, therefore, chimerism development substantially.42-46 It will be a challenge to use simulation studies to find out which of the model parameters might be related to those genes. Yet another process to investigate is how aging of stem cells translates into age-dependent changes of the model parameters.
Although our simulation results are widely confirmed by experiments that particularly focus on stem cell–specific, long-term effects, there are limitations with respect to short-term effects induced by cytokine stimulation and cytotoxic treatment. To correctly describe these effects it would be necessary to incorporate the development of lineage-restricted precursor cell stages and their dynamic feedback regulation into the model. A mathematical description of granulopoiesis has recently been published by our group.47 Although the granulopoiesis model has been adjusted for the human situation, the plan is to link these 2 model classes to arrive at a comprehensive model of hematopoiesis including the dynamics of stem cells and differentiated cells as well as interaction effects between them.
In contrast to classical stem cell concepts, which rely on a predefined differentiation hierarchy,48-53 our model describes stem cell organization as a self-organizing process. We interpret the observed heterogeneity and (hierarchical) structure of the hematopoietic stem cell population52,54-56 as emerging system properties rather than predefined cellular traits. Therefore, stem cell or repopulating potential can only be specified relative to the current state and to the context of the cells. Furthermore, it is not sufficient to specify the number of potential stem cells to characterize a population of cells, because their repopulation potential might change (eg, in response to another assay system). Within our concept, the reversible change of cellular properties is regarded as an essential mechanism to achieve a self-renewing stem cell population. In this sense, our model is covering plasticity phenomena of cellular properties57-59 in a natural way.
We like to emphasize that the proposed model can be considered in several respects as an extension of the stochastic stem cell model previously suggested by Abkowitz and coworkers in a seminal series of papers.21,22,60 Our model, though, is more general in describing a dynamically regulated stem cell pool that applies to steady state and non–steady state situations in vivo as well as to growth situations in in vitro assay systems. By taking cell-environment interactions into account, our model introduces explicitly a microscopic process (ie, transition between growth environments) explaining the self-renewal ability of stem cells. This mechanism automatically generates a heterogeneity of stem cells (regarding the homing affinity, a), which translates into functional differences (ie, self-renewal potential). Furthermore, our implementation of the stochastic model is not only able to describe the development of cell populations but, also, fates of individual cells, which enables the analysis of clone-tracking data.17,19,23
Taking the specific experimental setup into account, the presented simulation studies demonstrate that the proposed dynamic model is able to consistently explain clonal competition processes assuming strain- (or even clone-) specific differences in the dynamic control of stem cell proliferation and differentiation. We conclude that the concept of within-tissue plasticity provides a new, consistent theory to explain tissue stem cell organization as a dynamic, self-organizing process.
Prepublished online as Blood First Edition Paper, September 16, 2004; DOI 10.1182/blood-2004-01-0282.
Supported by the DFG (Deutsche Forschungsgmeinschaft), grant LO 342/9-1, and by the Netherlands Organization for Scientific Research (NWO), grant 901-08-339.
I.R. and L.M.K. contributed equally to this study.
The online version of the article contains a data supplement.
The publication costs of this article were defrayed in part by page charge payment. Therefore, and solely to indicate this fact, this article is hereby marked “advertisement” in accordance with 18 U.S.C. section 1734.

This feature is available to Subscribers Only
Sign In or Create an Account Close Modal