Abstract
For the past decade, it has become commonplace to provide rapid answers and early patient access to innovative treatments in the absence of randomized clinical trials (RCT), with benefits estimated from single-arm trials. This trend is important in oncology, notably when assessing new targeted therapies. Some of those uncontrolled trials further include an external/synthetic control group as an innovative way to provide an indirect comparison with a pertinent control group. We aimed to provide some guidelines as a comprehensive tool for (1) the critical appraisal of those comparisons or (2) for performing a single-arm trial. We used the example of ciltacabtagene autoleucel for the treatment of adult patients with relapsed or refractory multiple myeloma after 3 or more treatment lines as an illustrative example. We propose a 3-step guidance. The first step includes the definition of an estimand, which encompasses the treatment effect and the targeted population (whole population or restricted to single-arm trial or external controls), reflecting a clinical question. The second step relies on the adequate selection of external controls from previous RCTs or real-world data from patient cohorts, registries, or electronic patient files. The third step consists of choosing the statistical approach targeting the treatment effect defined above and depends on the available data (individual-level data or aggregated external data). The validity of the treatment effect derived from indirect comparisons heavily depends on careful methodological considerations included in the proposed 3-step procedure. Because the level of evidence of a well-conducted RCT cannot be guaranteed, the evaluation is more important than in standard settings.
Introduction
In oncology, new classes of anticancer agents have become an increasingly available and promising treatment option in several cancer indications, looking for precision cancer treatment.1 The development of these innovative therapies, such as molecularly-targeted agents, has led to an important modification in the evaluation process of cancer drugs, with an apparent need to improve the speed and efficiency of drug development. This has changed the way tolerance2 and antitumor activity3 are assessed in clinical trials, especially for early-stage trials. In contrast to the standard and separated phase I-II-III trials, accelerating clinical research with fewer patients involved and reduced costs may appear justified from the perspectives of both patients and public health.4 To this aim, single-arm trials are growingly reported as the sole basis for evaluating the efficacy of cancer drugs, mostly based on a surrogate end point,5 and this impacts the whole approval pathway.6 This observation is in line with the implementation of accelerated approval mechanisms by regulatory agencies such as the Food and Drug Administration -breakthrough therapy designation and European Medicines Agency -accelerated assessment. However, the approval of those therapies is based on weak or limited evidence.7,8 This is one of the reasons Health Technology Assessment bodies struggle to approve the reimbursement of these treatments associated with weak evidence compared with the gold standard. This was notably exemplified with immune checkpoint inhibitors, where 9 of the 10 accelerated approvals involved single-arm trials with the response rate as the main end point.6,9 However, the effect size of new molecules is mostly small, based on poorly relevant outcomes such as tumor response,10 though, in most settings, it has not been demonstrated that improving response yields an improvement in survival. The open nature of the design may introduce additional classification biases.11,12 This may explain why no benefit in overall survival has been demonstrated so far for many oncology drugs.5
Besides the study of drugs for registrational purposes, it is often reported that randomized clinical trials (RCT) may not be feasible or practical for rare diseases and biomarker-specific selected populations of more common diseases owing to ethical considerations, the requirement of large sample sizes, and extended durations of time.10,11 However, contrarily to situations of quasi-deterministic disease evolution, where nearly 0 or 100% of patients respond, relying on the observed “before-after” patient status to define a treatment effect is well known to be biased.13
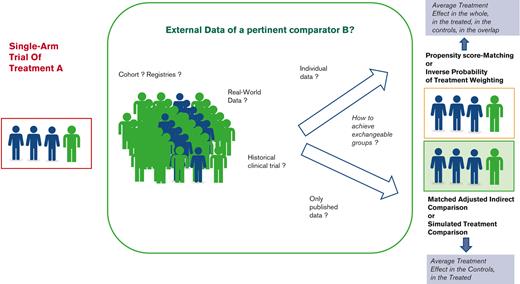
To handle the variability in the disease course as well as the unobserved effects of being enrolled in a trial, the measure of treatment effect requires to be relative to a control group. Thus, to increase the level of evidence in these uncontrolled settings, the use of external controls has been promoted.14 Such indirect comparisons are being growingly reported.15-18 However, as recently reported,19 they require careful implementation of innovative statistical methods accounting for between-group variation and selection biases, depending on the availability and nature of external data.20 Although many authors warned against the misuse of each approach and methodological issues from the use of external controls,21-24 none have detailed the whole process, including the underlying assumptions for leveraging those data.24
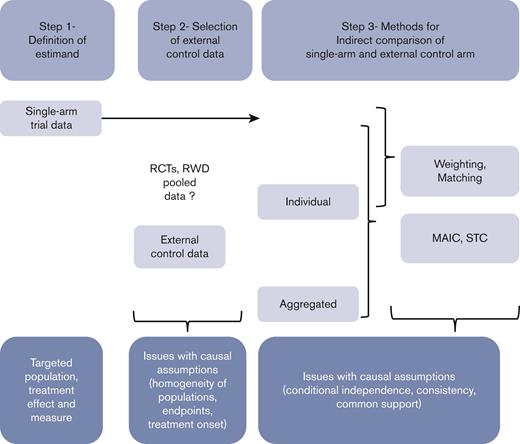
In this paper, we aim to provide some guidance for clinicians, investigators, manufacturers, and all stakeholders, highlighting the main issues of such external incorporations into single-arm trial data, and distinguishing a 3-step process (Figure 1). First, the specifications of key attributes or “estimands”, in line with the objectives, should be defined according to the principles of such “emulated” target trials. Second, the selection of the controls should consider the various sources of external controls to adequately mimic the lacking randomized experiment while avoiding substandard control arms. Specific statistical considerations may arise, according to the data type and characteristics. The last step consists of the indirect comparison itself, based on different methods according to the available data and the targeted treatment effect. A motivating example is used to illustrate this 3-step process.
Schematic 3-step process to be applied when incorporating external control data into single-arm trial data to maximize the validity of indirect comparisons.
Schematic 3-step process to be applied when incorporating external control data into single-arm trial data to maximize the validity of indirect comparisons.
Illustrating example
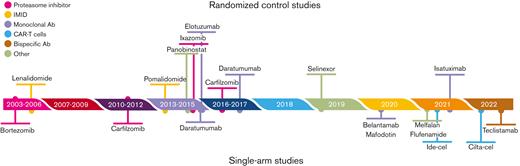
As an illustrative example, we used ciltacabtagene autoleucel (CARVYKTI; Janssen Biotech, Inc., Horsham, PA) approved by the Food and Drug Administration in February 2022 for the treatment of adult patients with relapsed or refractory multiple myeloma (RRMM) after 3 or more prior lines of therapy, including a proteasome inhibitor (PI), an immunomodulatory agent (IMiD), and an anti-CD38 monoclonal antibody. The pivotal trial was CARTITUDE-1 (NCT03548207), a multicenter, phase 1b/2 open-label, single-arm, clinical trial conducted in the United States between July 2018 and October 2019.25 A total of 113 patients with RRMM, with at least 3 prior lines of therapy including a PI, an IMiD, and an anti-CD38 monoclonal antibody, and disease progression on or after the last regimen were enrolled. Among the 113 enrolled patients, 97 (85.8%) patients who received ciltacabtagene autoleucel (cilta-cel) were included in the analysis. The efficacy was established based on the overall response rate (ORR) as the main end point, estimated at 97% (95% confidence interval [CI], 91.2-99.4). However, RRMM, especially the triple-class-refractory disease, is an extremely active area of research, in which many drugs that may act as pertinent comparators have been proposed. Indeed, in that population, many drugs from distinct classes have been approved by the FDA, including monoclonal antibodies such as belantamab mafodotin,26 isatuximab,or teclistamab,27 small molecule inhibitors/modulators such as selinexor,28 or melphalan flufenamide,29 or other CAR T cells such as idecabtagene vicleucel (ide-cel)25 (Figure 2). We will show how indirect comparisons can be performed and findings can be achieved on the relative efficacy of cilta-cel.
Timeline of the drugs approved by the FDA for the treatment of patients with RRMM.
Timeline of the drugs approved by the FDA for the treatment of patients with RRMM.
Step 1- definition of estimands
An estimand is a precise description of a treatment effect reflecting a clinical question that should inform study design and analysis under 5 attributes: target population, treatment, end point, intercurrent events, and population level summary of the treatment effect measured against some valid comparator. First described for RCTs,30 its principles can be easily extended to observational studies.31,32
Rarely, the treated and control populations can be assumed similar, owing to similar eligibility criteria, time period, and the sites of enrolment.33 To overcome this issue, down weighting the external control data allows to decrease the level of evidence from the external source to be addressed using either power prior models34-36 or meta-analytic approaches.22
However, most of the time, populations differ in characteristics that may also affect the outcome, these are termed “confounders” (Box 1). Ignoring those differences will lead to misleading inferences owing to confounding bias.37 Indeed, any differences in outcomes could no longer be attributed to differences in treatments but rather to confounders.
Thus, reaching a balance in confounder population is at the core of causal inference in observational studies. Regression models providing estimates of the treatment effect adjusted on prognostic factors have been long used for that purpose. However, they do not ensure a balance of prognostic variables across groups, notably, where their values widely differ across groups; in these areas of nonoverlap, estimates are extremely sensitive to model choices. Thus, rather than focusing on the outcome model (by introducing both treatment and confounders to predict the outcome), one may focus on the treatment model through the propensity score (PS), that is, the probability of being in the treatment group, conditional on the set of observed confounders.38 Then, individuals are given individual “balancing” weights,31 derived from their PS, to under- or overrepresent the characteristics of their treatment group compared with the other group (Figure 3). Under different assumptions of conditional independence, consistency, and common support (Box 2), valid estimators of the treatment effect can be directly derived from the weighted data. The main advantage of the propensity score is to separate the treatment model and the outcome model. Modelling the treatment probability further forces one to think about the imbalances in covariates before estimating the treatment effect.
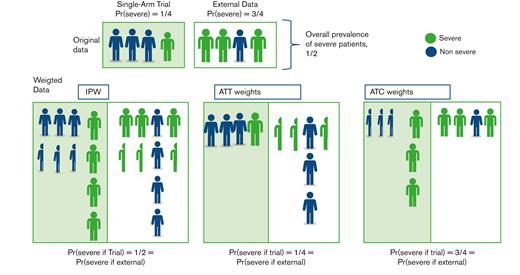
Schematic representation of how data are weighted according to an estimand. Suppose the original sample from the single-arm trial differs from the external controls in terms of patient severity, with 1 severe case over 4 in the trial compared with 3 over 4 in the external data. The objective is to modify the pooled data to obtain 2 groups where the proportion of severe cases is similar. Most methods are based on the PS, which is the probability of each patient being in the trial, conditional on their severity. In this setting, each severe case is given a PS of 1/4, whereas each nonsevere case is given a PS of 3/4. IPW consists of inversely weighting each individual in the original sample according to their probability of being in the original group, that is, for the treated, the individual contribution of each patient is divided by their PS (thus resulting in adding 1/3 of a fictive patient for each nonsevere patient and 3 fictive individuals for severe cases), while in the external group, this value is divided by 1 minus their PS (thus adding 1/3 of a fictive patient for each severe patient and 3 fictive individuals for each nonsevere case). This yields a weighted sample where the proportion of severe cases is similar in both groups (1/2) and differs from that in both original groups. ATT weights consist of using all individuals from the single-arm trial (weight of 1) and weighting each individual in the external sample by the odds of being in the trial. This results in odds of (1/4)/(3/4) = 1/3 in nonsevere cases and (3/4)/(1/4) = 3 in severe cases, reaching a ¼ prevalence of severe cases in the pooled weighted data set, that is, observed in the originally treated patients from the trial. ATC weights are conversely computed, with a weight of 1 for each patient from the external sample, whereas patients from the single-arm trial are given a weight of (3/4)/(1/4) (severe cases) or (1/4)/(3/4) (nonsevere cases). The resulting prevalence of severe cases is now that of the original external control group, that is, 3/4.
Schematic representation of how data are weighted according to an estimand. Suppose the original sample from the single-arm trial differs from the external controls in terms of patient severity, with 1 severe case over 4 in the trial compared with 3 over 4 in the external data. The objective is to modify the pooled data to obtain 2 groups where the proportion of severe cases is similar. Most methods are based on the PS, which is the probability of each patient being in the trial, conditional on their severity. In this setting, each severe case is given a PS of 1/4, whereas each nonsevere case is given a PS of 3/4. IPW consists of inversely weighting each individual in the original sample according to their probability of being in the original group, that is, for the treated, the individual contribution of each patient is divided by their PS (thus resulting in adding 1/3 of a fictive patient for each nonsevere patient and 3 fictive individuals for severe cases), while in the external group, this value is divided by 1 minus their PS (thus adding 1/3 of a fictive patient for each severe patient and 3 fictive individuals for each nonsevere case). This yields a weighted sample where the proportion of severe cases is similar in both groups (1/2) and differs from that in both original groups. ATT weights consist of using all individuals from the single-arm trial (weight of 1) and weighting each individual in the external sample by the odds of being in the trial. This results in odds of (1/4)/(3/4) = 1/3 in nonsevere cases and (3/4)/(1/4) = 3 in severe cases, reaching a ¼ prevalence of severe cases in the pooled weighted data set, that is, observed in the originally treated patients from the trial. ATC weights are conversely computed, with a weight of 1 for each patient from the external sample, whereas patients from the single-arm trial are given a weight of (3/4)/(1/4) (severe cases) or (1/4)/(3/4) (nonsevere cases). The resulting prevalence of severe cases is now that of the original external control group, that is, 3/4.
When comparing single-arm vs external control groups, these methods could be used. However, the target population should first be defined, as this definition impacts the definitions of weights and the targeted treatment effect (Table 1). Indeed, one may focus on the average treatment effect (ATE) in the population represented by the combined single-arm and external control groups that would be observed by switching every unit in the whole population from one treatment to the other, the average treatment effect in the treated (ATT), obtained by only switching the treated to the control group; or the average treatment effect in the control (ATC).
Targeted population, weights, and estimands
| Method for controlling confounders . | Weights for treated, untreated . | Target population . | Estimand . |
|---|---|---|---|
| Inverse weighting | Combined from the treated and untreated | ATE | |
| 1, | Treated population | ATT | |
| Control population | ATC | ||
| 1-e | Overlapping population | ATO | |
| Trimming population | Not specified | ||
| Matching | Matching population | ATT | |
| Matching-adjusted indirect comparison | Control population | ATC |
| Method for controlling confounders . | Weights for treated, untreated . | Target population . | Estimand . |
|---|---|---|---|
| Inverse weighting | Combined from the treated and untreated | ATE | |
| 1, | Treated population | ATT | |
| Control population | ATC | ||
| 1-e | Overlapping population | ATO | |
| Trimming population | Not specified | ||
| Matching | Matching population | ATT | |
| Matching-adjusted indirect comparison | Control population | ATC |
is the propensity score, where T = 1 for the single-arm treatment group, T = 0 for the external control group, and V is the set of observed confounders in both groups.
ATO, average treatment effect in the overlap population.
For instance, when evaluating the benefit of cilta-cel over some pertinent comparator in the patients with RRMM, the ATE, corresponding to switching every unit in the study population from the comparator to cilta-cel and reciprocally, may result in the effect of an infeasible intervention. In contrast, choosing the ATT targets the treated population, that is, those included in the single-arm trial and attempts to answer “what would have been the ORR of the patients treated with cilta-cel, had they all received the comparator instead?”. This may be the estimand of interest in this setting, and it was mostly used in the published indirect comparisons of cilta-cel against standard treatment.39-41 The ATC provides the alternate answer to “what should have been the ORR in the patients from the comparator group had they received cilta-cel instead?”. Such an estimand was used to assess the benefit of cilta-cel against active comparators, though not reported as such.42,43
Step 2- selection of the external control data
Then, one may look for external, sometimes called “synthetic”,44 controls. In line with the objective, the closeness of the external population with the targeted population should be first required to avoid the risk of substantial biases. This could be evaluated using the acceptability criteria proposed by Pocock.33 The selection of external controls should use predefined eligibility criteria for the inclusion of studies to ensure patient similarity, relevant end points, and pertinent comparators.
External controls could be directly selected from pertinent and efficacious active arms from previously completed RCTs20 or reconstituted from real-world data (RWD).45
When external controls are selected from RCTs, it is likely that the potential comparator has been sponsored by another firm, so only aggregated data are available. Pooled data from previous RCTs could also be used as external controls, as exemplified by the FDA that approved a synthetic control generated from more than 22 000 previous studies to be used in a phase III glioblastoma cancer trial.46
When no available controls from previous trials are available, controls can be selected from RWD, including observational cohorts, registries, or electronic health records (EHR),47 as well as claims and prescription data.48 Although primary end points may be difficult to match in RWD and clinical trials, it is not the case in cancer where the date of death is usually reported in the EHR or any administrative registry. To control for the potential effects of time and center, an adequate selection of both should be considered first.49 The closeness of populations is of particular concern in the observational setting in which the choice of treatment based on a patient’s disease status achieves a “confounding-by-indication” bias. In many chronic diseases, there is also no obvious single timepoint for treatment decisions.49 Thus, when the population differs in terms of the time of treatment decision-making, “immortal time bias” or “time-lag bias” could be additionally introduced.49 Once sources of control data are found, their validity should be measured by assessing the risk of bias. As reported recently, based on publicly available FDA reviews of medical products, most reasons why RWD did not contribute to regulatory decision-making relied on a lack of a prespecified study design and analysis as well as data reliability and relevancy concerns.50
In the cilta-cel example, several indirect comparisons in patients with RRMM were secondarily published, as summarized in Table 2. They first used conventional treatment as the comparator of interest, with data obtained from long-term follow-up of previous clinical trials,39 or multicenter retrospective studies,41 and RWD.40 However, the clinical relevance of such a “standard treatment” group may be questioned because of targeting a very heterogenous and frail population that may not be a candidate for CART-cell therapy. Moreover, the use of retrospective studies and RWD raises the issue of data quality (data do not undergo the same level of quality checks as in the trial), resulting in the selection, measurement, and attrition biases. Last, CAR T cells are administered after a variable period on potentially selected patients. This raises concerns about the comparison with those cohorts, with different start dates of follow-up.51
Illustration of the 3-step assessment on the main indirect comparisons of celta-cel against comparators. Bold cells indicate the main issues of the performed comparisons. The following 5 main confounders were considered and ranked as major confounders by experts: Refractory status, cytogenetic profile, R-ISS stage, plasmacytomas, and time to progression on last prior line
| Indirect comparison . | Step 1- Estimand . | Step 2- External source of data . | Step 3- Methods of comparison . | |||||
|---|---|---|---|---|---|---|---|---|
| Main objective . | Comparator . | Type . | Source . | Propensity score . | Method . | Balance diagnostics, common support . | Estimation of effect . | |
| Merz 2021 | ATT | Standard treatment heterogeneity | IPD | Retrospective German RWD database risk of bias | 9 confounders∗ cytogenetic and plasmacytomas missing | IPW | Undetailed “remaining imbalances” (SMD >0.20) | Weighted analyses with robust variance |
| Weisel 2022 | ATT | Physician choice heterogeneity | IPD | Follow-up of trial data (POLLUX, CASTOR, EQUULEUS) | 8 confounders† | IPW | Mean SMD reduced from 0.33 to 0.16 | Weighted analyses with robust variance |
| Costa 2022 | ATT | Conventional treatment heterogeneity | IPD | Retrospective study Risk of bias | 16 confounders‡ Plasmacytomas missing | Matching 1:1, no replacement, caliper 0.05 | SMD between 0.10 and 0.20 (ASCT, refractory to carfilzomib, penta-drug refractory) | Stratified/weighted analyses |
| Weisel 2022 | ATC not explicitly reported | Belantamab mafodotin | Aggregate | One-arm (2.5 mg/kg dose) of the 2-arm trial data (DREAMM-2) ECOG 0-2 | 4 confounders § Time to progression on the last regimen missing | Unanchored MAIC | ESS = 39 (60% reduction) no report of weight distribution | Weighted analyses |
| ATC not explicitly reported | Selinexor-DXM | Aggregate | RCT data (mITT of STORM-2) Penta-exposed ECOG 0-2 | 4 confounders § Time to progression on the last regimen missing | Unanchored MAIC | ESS = 73 (25% reduction) No report of weight distribution | ||
| ATC not explicitly reported | Melphalan-flufenamide-DXM | Aggregate | A subset of Single-arm trial data (HORIZON) received ≥2 prior LOTs ECOG 0-2 | 3 confounders refractory status missing | Unanchored MAIC | ESS = 85 (12% reduction) no report of weight distribution | ||
| Martin 2022 | ATC not explicitly reported | Ide-cel | Aggregate | Single-arm trial data (KarMMa) | 4 confounders § Time to progression on the last regimen missing | Unanchored MAIC | Skewed distribution of weights ESS: 46%-57% reduction | Weighted analyses failure times measured from cells infusion |
| Indirect comparison . | Step 1- Estimand . | Step 2- External source of data . | Step 3- Methods of comparison . | |||||
|---|---|---|---|---|---|---|---|---|
| Main objective . | Comparator . | Type . | Source . | Propensity score . | Method . | Balance diagnostics, common support . | Estimation of effect . | |
| Merz 2021 | ATT | Standard treatment heterogeneity | IPD | Retrospective German RWD database risk of bias | 9 confounders∗ cytogenetic and plasmacytomas missing | IPW | Undetailed “remaining imbalances” (SMD >0.20) | Weighted analyses with robust variance |
| Weisel 2022 | ATT | Physician choice heterogeneity | IPD | Follow-up of trial data (POLLUX, CASTOR, EQUULEUS) | 8 confounders† | IPW | Mean SMD reduced from 0.33 to 0.16 | Weighted analyses with robust variance |
| Costa 2022 | ATT | Conventional treatment heterogeneity | IPD | Retrospective study Risk of bias | 16 confounders‡ Plasmacytomas missing | Matching 1:1, no replacement, caliper 0.05 | SMD between 0.10 and 0.20 (ASCT, refractory to carfilzomib, penta-drug refractory) | Stratified/weighted analyses |
| Weisel 2022 | ATC not explicitly reported | Belantamab mafodotin | Aggregate | One-arm (2.5 mg/kg dose) of the 2-arm trial data (DREAMM-2) ECOG 0-2 | 4 confounders § Time to progression on the last regimen missing | Unanchored MAIC | ESS = 39 (60% reduction) no report of weight distribution | Weighted analyses |
| ATC not explicitly reported | Selinexor-DXM | Aggregate | RCT data (mITT of STORM-2) Penta-exposed ECOG 0-2 | 4 confounders § Time to progression on the last regimen missing | Unanchored MAIC | ESS = 73 (25% reduction) No report of weight distribution | ||
| ATC not explicitly reported | Melphalan-flufenamide-DXM | Aggregate | A subset of Single-arm trial data (HORIZON) received ≥2 prior LOTs ECOG 0-2 | 3 confounders refractory status missing | Unanchored MAIC | ESS = 85 (12% reduction) no report of weight distribution | ||
| Martin 2022 | ATC not explicitly reported | Ide-cel | Aggregate | Single-arm trial data (KarMMa) | 4 confounders § Time to progression on the last regimen missing | Unanchored MAIC | Skewed distribution of weights ESS: 46%-57% reduction | Weighted analyses failure times measured from cells infusion |
ASCT, allogeneic stem cell transplantation; DXM, dexamethasone; ECOG, Eastern Cooperative Oncology Group; ISS, international staging system; LOT, line of treatment; MM, multiple myeloma.
Age, sex, refractory status, R-ISS stage, time to progression on last prior line, number of prior LOTs, average duration of prior lines, years since diagnosis, ECOG status.
Age, refractory status, ISS stage, cytogenetic profile, time to progression on last regimen, plasmacytoma, number of prior LOTs, years since MM diagnosis.
Age, sex, race/ethnicity (white vs other), ISS stage 3 (vs 1, 2, or unknown), time from diagnosis to index date, number of prior LOT, prior autologous stem cell transplant, presence of high- risk cytogenetic abnormalities in any prior sample [t(4;14), t(14;16), del(17p)], refractoriness to bortezomib or ixazomib, refractoriness to carfilzomib, refractoriness to lenalidomide, refractoriness to pomalidomide, refractoriness to anti-CD38 monoclonal antibody, triple-class refractoriness, penta-drug exposure (to bortezomib or ixazomib plus carfilzomib plus lenalidomide plus pomalidomide plus anti-CD38 monoclonal antibody), and penta-drug refractoriness.
Refractory status, cytogenetic profile, R-ISS stage, plasmocytomas.
More recently, 2 indirect comparisons focused on more pertinent active comparators, recently approved by the FDA at the time cilta-cel was proposed (Figure 2), namely belantamab mafodotin and melphalan flufenamide, each assessed from a single-arm trial or selinexor, using RCT data42 and ide-cel, another CAR T-cell therapy.43 Given that the data of these control groups were prospectively recorded in clinical trials, it likely improved the control of other sources of bias compared with RWD.
Step 3- methods for indirect comparisons of single-arm and external control arms
Last, an indirect comparison of the single-arm trial and the external control arm should be performed using appropriate statistical methods, and underlying assumptions should be checked. Such methods mostly depend on whether the control data have been measured at the individual level or aggregated level.
Individual-level external control data
The availability of individual-level data for both groups allows the PS to be estimated to balance the confounders of the treated (trial) group and the (external) control group using weighting or matching (Table 1). When the external individual-level data are obtained from observational data, additional weights may be used to incorporate the decreased level of evidence of the controls.52
The most common approach to estimate the inverse probability of treatment weights (IPWs) is to estimate the PS through logistic regression, ideally including all the true confounders, then directly definining weights for both the treated and control population. Such weights target the ATE of the underlying population defined by the combination of the treated and untreated groups (Figure 3). Unfortunately, the “convenience” sample defined by the pool of the trial sample and the external controls, does not always represent a population of scientific interest, in contrast to surveys from which such methods have been derived. To focus on the treated population and estimate the ATT, only control patients are given a weight depending on the odds of being treated whereas treated patients are given a unit weight.
For both types of weights, the challenge associated with extreme propensities has been identified as a primary downside of weighting, with no clear definition of the resulting ambiguous target population.53 Methods that address nonoverlap, such as trimming or downweighting data in regions of poor data support, excluding or censoring weights at some extreme percentiles, change the estimand so that inference cannot target the population of interest. Thus, balancing weights has been proposed as a simple way to define, based on specific tilting functions, individual weights, and the resulting target population,54 as it integrates most approaches, including PS matching.38 Recently, “overlap weights” were proposed to focus on the population for which observed confounders have been adequately balanced (Table 1). Finally, it should be noted that all those weighted samples differ in terms of the target population, as illustrated in the observed patient characteristics, either close to those of the pooled groups, of the treated, the controls, or the overlapping sample (Figure 2). In all cases, the exchangeability of the restructured groups should be measured, using simple measures such as standardized mean difference (SMD) which should be below 10% (as a rule-of-thumb) or any other distances.55
In the indirect comparisons of cilta-cel vs observational cohorts or RWD,39-41 individual patient data were available to estimate PS from multivariable logistic models, then using either matching41 or weighting,39,40 to estimate the ATT. However, none of these comparisons fulfilled all those “quality” requirements (Table 2). Notably, confounders included in the propensity score were not fully reported or did not include all expert knowledge of true confounders. All analyses failed to reach a clearcut exchangeability of groups, with reported persistent imbalances (either not detailed or with SMDs above 15% for several confounders). This resulted in a risk of bias for the estimated cilta-cel effect.
Aggregated external control data
When control data are derived from clinical trials not sponsored by the manufacturer’s product of the single-arm trial, it is not uncommon for only published aggregate data to be available. In this setting, only summary measures of both the confounders and outcomes are at most available. Notably, for time-to-event data, some types of individual-level data can be extracted from published Kaplan–Meier curves using digitization,56 but individual-level data on confounders would still not be obtained. To address such aggregated control data, population-adjusted indirect comparisons have been proposed, the 2 most popular methods being matching-adjusted indirect comparison (MAIC)57 and simulated treatment comparison (STC).58
MAIC is a reweighting method similar to IPW that targets the control population. Its principle is to reweigh the individual-level data such that the mean characteristics of the treated population are balanced with those of the controls, with weights estimated from the PS of being treated. The resulting target population is that of the external data set, thus, allowing the estimation of the ATC (Table 1). Notably, the PS cannot be estimated as usual given the lack of individual patient data for the controls, but alternate methods can be used.59 It is then important to evaluate the distribution of weights, which should be centered around 1. If there are too many participants being allocated near zero or very high weights, the comparability of groups is questioned, with increased uncertainty of the results. The effective sample size (ESS) can also be computed as a measure of information provided by the weighted data set. A small ESS, relative to the original sample size, is an indication that the weights are highly variable and that the estimate may be unstable. In STC, individual-level data are used to model the relationship between predictors and outcome of the single-arm trial, and then the model is used to estimate the outcomes in external controls.
Both MAIC and STC rely on the strong assumption of a constant absolute treatment effect at any level of the effect modifiers and prognostic variables and that all effect modifiers and prognostic variables have been observed, otherwise, the estimates are biased.58 Thus, providing information on the likely biases resulting from unobserved prognostic factors and effect modifiers distributed differently across the trials is mandatory. Such indirect comparisons require additional recommendations. First, evidence that absolute outcomes can be predicted with sufficient accuracy in relation to the relative treatment effect should be provided. Moreover, the choice of the outcome scale is critical and should be justified because the effect modifier status is scale specific. An important limitation is that MAIC or STC is only able to provide estimates in the target population represented by the external comparator population and not that of the single-arm trial of interest. For any other target population, a supplementary assumption, the shared effect modifier, is needed.58
Two unanchored MAICs were published to compare the effect of cilta-cel with active pertinent comparators from single-arm clinical trials.42,43 Only the 97 patients infused by cilta-cel were selected. Except when compared with other CAR T cells, a potential selection bias of the treatment group can be suspected, given the 16 patients who could not be reinfused owing to disease progression (n = 2), death (n = 9), or patient withdrawal (n = 5), were excluded.25 None of the MAICs included the 5 “true” confounders selected by the experts, so the underlying assumption of no unmeasured confounders is possibly violated. Moreover, the distribution of the weights and the weighted baseline characteristics were not fully reported, whereas the reduction in the effective sample size of the cilta-cel–treated population was relatively high, from 46% to 60%, resulting in the ESS being down to 39 (Table 2). It indicates that there may be poor overlap between the study populations, violating the underlying assumption of common support (illustrating the potential selection bias described above), again resulting in a high risk of bias.
Discussion and perspectives
The provision of rapid answers when evaluating a new treatment outside the standard phase I-III strategy is becoming increasingly important.60 Currently, the use of single-arm clinical trials as the sole source of evidence provided by pharmaceutical firms to obtain, at least temporaririly, drug approvals, is accepted by regulatory agencies for populations or individuals with certain indications. This is also widely used by academics when evaluating interventions in rare cancer subgroups or combination therapies.61 This may appear contradictory to the statistical literature reporting its many sources of bias since the early 1980s.62
There could be some ways of improving the value of data and thus increasing the utility of single-arm trials.63 Thus, to decrease the uncertainty of such uncontrolled trials, comparisons using external controls have been growingly reported in oncohematology, for instance, in acute lymphoblastic leukemia,15 large B-cell lymphoma,64 anaplastic lymphoma,17 follicular lymphoma,18 metastatic nonsmall-cell lung cancer,65 endometrial cancer,16 and glioblastoma.66 Such indirect comparisons require a complex implementation to be valid, as recently reported.67 In the specific setting of single-arm trials, we aimed to report how to enhance the evidence from such trials by incorporating and leveraging external data as a “synthetic” control arm to mimic the lacking “head-to-head” comparison. Thus, we provided some guidance for incorporating such external controls by defining a 3-step process to stop the sequence whenever a target or underlying assumption could not be satisfied. First, the target population, pertinent comparator, and measure of the treatment effect should be clearly delineated. Second, the selection of the target controls should be carefully and adequately performed with respect to the population, end point and treatment decision. Indeed, using controls from previous RCT or other trials is likely different than defining controls from RWD, from which selection of pertinent patients raises issues, notably concerning the immortal time bias and reverse causation issues. This raises the issue of sharing individual patient data so that the secondary use of available health data should be promoted, which begins by encouraging secure and facilitated access to those data by researchers worldwide, as proposed by the American Society of Hematology’s Research Collaborative.45 Last, the method of analysis should be justified based on the type of available data and on the underlying target population and the therapeutic question of interest (eg, to treat all patients or not?). The use of external controls finally entails merging different sources of data, which may complicate the verification of causal assumptions and not adequately control for confounding factors, which is a necessary but not sufficient framework for valid estimation of treatment effect. Indeed, although treatment groups achieved by random allocation are exchangeable in terms of all (observed or not) prognostic covariates and treatment-effect modifiers, PS methods could only rely on the observed confounders, their main limitation, even if the analysis is well conducted. Nevertheless, well-conducted indirect comparisons may generate hypotheses for new trials regarding pertinent comparators and thus may appear as an option while or before an RCT is conducted.
In all cases, especially given the risk that analyses would be data-driven and adapted ad hoc, the statistical analysis plan for such incorporation should be publicly issued before the analysis, and only external controls recruited after that publication should be used in the comparisons in a similar approach as in registered reports.68 The principled framework of emulating a target trial combining the principles of clinical trials and causal methods to control for confounding appears particularly adequate in this situation.69,70
We mostly considered methods derived from propensity scores, although other approaches could also be considered, such as g-computation,71 or “double-robust” or “augmented IPW” estimators.72 To the best of our knowledge, these approaches have not been used for regulatory approval with external controls but remain promising alternatives. Other issues, such as time-dependent biases, may exist as well.49 How to adequately control for time-dependent biases with external controls is still an open issue.
In summary, when reporting results from a single-arm trial, the provision of some external comparison to controls is often reported, with the aim to obtain marketing authorization. In all cases, it should be adequately done and reported to provide evidence. It should be kept in mind that such indirect comparisons aim to mimic the lacking randomized clinical trials. Only respect for the proposed 3-step guidance may provide a correct level of evidence, although it cannot be guaranteed that it will reach the level of a well-conducted RCT.
Authorship
Contribution: S.C. was responsible for supervision and project administration and visualization; and all authors worked on the conceptualization, data curation, methodology, formal analysis, resource writing of the original draft, review, and editing of the manuscript.
Conflict-of-interest disclosure: The authors declare no competing financial interests.
Correspondence: Sylvie Chevret, Biostatistics and Medical Information Service (SBIM)-Saint Louis Hospital, 1 Ave Claude Vellefaux 75010 Paris, France; e-mail: sylvie.chevret@u-paris.fr.