Key Points
Stacked ensemble of machine-learning algorithms could establish more accurate prediction model for survival analysis than existing methods.
Stacked ensemble model can be applied to personalized prediction of HSCT outcomes from pretransplant characteristics.
Abstract
Graft-versus-host disease-free, relapse-free survival (GRFS) is a useful composite end point that measures survival without relapse or significant morbidity after allogeneic hematopoietic stem cell transplantation (allo-HSCT). We aimed to develop a novel analytical method that appropriately handles right-censored data and competing risks to understand the risk for GRFS and each component of GRFS. This study was a retrospective data-mining study on a cohort of 2207 adult patients who underwent their first allo-HSCT within the Kyoto Stem Cell Transplantation Group, a multi-institutional joint research group of 17 transplantation centers in Japan. The primary end point was GRFS. A stacked ensemble of Cox Proportional Hazard (Cox-PH) regression and 7 machine-learning algorithms was applied to develop a prediction model. The median age for the patients was 48 years. For GRFS, the stacked ensemble model achieved better predictive accuracy evaluated by C-index than other state-of-the-art competing risk models (ensemble model: 0.670; Cox-PH: 0.668; Random Survival Forest: 0.660; Dynamic DeepHit: 0.646). The probability of GRFS after 2 years was 30.54% for the high-risk group and 40.69% for the low-risk group (hazard ratio compared with the low-risk group: 2.127; 95% CI, 1.19-3.80). We developed a novel predictive model for survival analysis that showed superior risk stratification to existing methods using a stacked ensemble of multiple machine-learning algorithms.
Introduction
Allogeneic hematopoietic stem cell transplantation (HSCT) is a potentially curative therapy for hematological malignancies, bone marrow (BM) failure syndromes, and immunodeficiency syndromes. Although the improvement in outcome has been confirmed by several studies, 2 serious risk factors remain for poor outcome: transplantation-related morbidity and mortality (TRM) and progression of diseases. Intensive treatment to overcome disease progression often leads to severe graft-versus-host disease (GVHD) and TRM; on the other hand, reduced-intensity conditioning can reduce TRM but increase relapse rate.1-4
Age, disease stage, donor type, and donor recipient gender combinations were reported to influence survival, nonrelapse mortality (NRM), and relapse risk. These pretransplant risk factors were identified from hypothesis-driven variable selection and validation using conventional statistical analysis. Various predictive scoring systems have also been established based on these findings. Hematopoietic cell transplantation–specific comorbidity index is used for assessment of pretransplant comorbidities.5 The European Group for Blood and Marrow Transplantation risk score consists of 6 pretransplant risk factors associated with relapse and GVHD.6 These scoring systems are used for clinical decision-making for HSCT indication or donor selection.
Machine learning is a field of computer science in which computer algorithms that have the ability to improve from experience without being explicitly programmed are studied. Machine-learning methods provide statistical calculations without the assumptions needed for traditional statistical analysis, so machine-learning–based prediction gives novel insights into clinical medicine. To predict prognosis of HSCT patients, early studies demonstrated the feasibility of machine-learning algorithms for binary outcomes, such as decision tree–based learning, artificial neural networks, and support vector machines.7-11 Recent reports applied machine-learning methods developed for right-censored data with or without competing risks for HSCT outcomes.12-14 Machine-learning methods are a useful way to predict time-dependent outcomes without assumptions, but how to improve predictive accuracy is still an ongoing discussion.
In this study, we developed a novel prediction model that appropriately handles right-censored data and competing risks using ensemble learning to predict composite end point of GVHD-free, relapse-free survival (GRFS).15
Materials and methods
Population
All transplantation data in Japan are annually collected at the Japanese Data Center for Hematopoietic Cell Transplantation. The Kyoto Stem Cell Transplantation Group (KSCTG), which is a multi-center group of 17 transplantation centers in Japan, received transplant data from the Japanese Data Center for Hematopoietic Cell Transplantation. From the registry database of KSCTG, we extracted clinical data for 2207 patients who underwent their first HSCT for hematologic malignancies between 1996 and 2016 in KSCTG hospitals. The study was conducted according to the Declaration of Helsinki and was approved by the institutional review boards at Kyoto University Hospital and all other participating centers.
End point and definitions
The primary end point was GRFS, and the secondary end points were overall survival (OS), relapse, NRM, and GVHD. GRFS was defined as the time from transplant to the last date of follow-up or event of grade III-IV acute GVHD, extensive chronic GVHD, relapse, or death.16 Relapse was defined based on the morphological and clinical evidence of disease activity, and NRM was defined as the time to death without relapse. Acute and chronic GVHD were diagnosed and graded using standard criteria.17,18 The intensity of the conditioning regimen was classified as myeloablative if total body irradiation >8 Gy, oral busulfan ≥9 mg/kg, IV busulfan ≥7.2 mg/kg, melphalan >140 mg/m2, or thiotepa ≥10 mg/kg was used in the conditioning regimen; otherwise it was classified as reduced intensity.19 We assessed disease risk using the refined disease risk index (DRI) established by the Center for International Blood and Marrow Transplant Research.20 The refined DRI does not establish adult T-cell leukemia/lymphoma (ATL) as an individual risk group. We regarded complete remission or partial remission ATL as intermediate risk and advanced ATL as very high risk. We categorized high-grade B-cell lymphoma with MYC and BCL2 and/or BCL6 rearrangements into the same group with Burkitt lymphoma due to its poor prognosis. DRI was retrospectively calculated based on the available registry data about diagnosis, chromosomal alterations, and staging before transplantation. Disease stage was defined as previously described.21
Outline of statistics
The following is a summary of the analysis outline: (1) preprocessing-data quality assurance and imputations of missing values, (2) construction of each prediction model, (3) development of a stacked ensemble model, and (4) assessment of the predictive performance of a stacked ensemble model in accordance with the Type 2a (random split-sample development and validation) of prediction model studies covered by the Transparent Reporting of a prediction model for Individual Prognosis Or Diagnosis statement.22 Missing values are imputed with median value of the nonmissing data for categorical variables and with mean value of the nonmissing data for continuous variables. A dummy variable is also generated, indicating whether the data were missing for that particular patient.
Establishment of stacked ensemble model
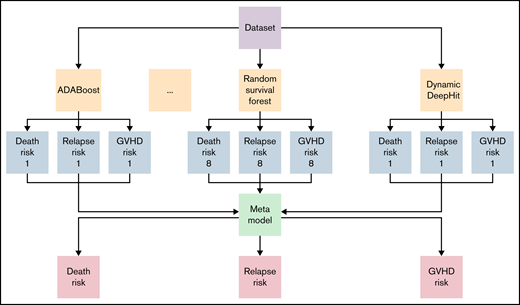
A stacked ensemble of multiple machine-learning algorithms for right-censored data was applied to develop a model. Formally, an ensemble model is a model that combines the predictions from multiple trained models. A stacked ensemble model is a variation of the ensemble method and uses an algorithm that takes the outputs of submodels as inputs and learns the optimal way to combine the input predictions.23 Predictions are first generated using different algorithms, including cause-specific Cox Proportional Hazard (Cox-PH), Random Survival Forest, Dynamic DeepHit, ADABoost, XGBoost, Extra Tree Classifier, Bagging Classifier, and Gradient Boosting Classifier.12,24 -31 A meta-model is subsequently trained, using these predictions as inputs, to generate the final prediction. Data were randomly split into the training set (70% of the dataset) and the validation set (30%). The model was trained and tested using a fivefold cross-validation on the training set. All models were trained using 26 input variables available from the registry data containing information on a patient’s underlying disease, donor source, and patient and donor’s demographic characteristics. Patient sex, source of stem cells, and diagnosis (Table 1) and variables (supplemental Table 1) were treated as categorical variables. Patient age and time from diagnosis to transplant (Table 1) and variables (supplemental Table 2) were treated as continuous variables.
Patient characteristics
| Variable . | Total . | Training set . | Validation set . | P . |
|---|---|---|---|---|
| n = 2207 (%) . | n = 1765 (%) . | n = 442 (%) . | ||
| Age group at transplant, y | .327 | |||
| ≤30 | 339 (15.4) | 265 (15.0) | 74 (16.7) | |
| >30-40 | 340 (15.4) | 277 (15.7) | 63 (14.3) | |
| >40-50 | 480 (21.7) | 376 (21.3) | 104 (23.5) | |
| >50-60 | 631 (28.6) | 509 (28.8) | 122 (27.6) | |
| >60 | 417 (18.9) | 338 (19.2) | 79 (17.9) | |
| Sex | .572 | |||
| Male | 925 (41.9) | 734 (41.6) | 191 (43.2) | |
| Female | 1282 (58.1) | 1031 (58.4) | 251 (56.8) | |
| Source of stem cells | .279 | |||
| BM | 1349 (61.1) | 1061 (60.1) | 288 (65.2) | |
| Peripheral blood | 356 (16.1) | 292 (16.5) | 64 (14.5) | |
| BM + peripheral blood | 7 (0.3) | 6 (0.3) | 1 (0.2) | |
| Cord blood | 495 (22.4) | 406 (23.0) | 89 (20.1) | |
| Time from diagnosis to transplant | .707 | |||
| ≤6 mo | 793 (35.9) | 638 (36.1) | 155 (35.1) | |
| >6 mo | 1392 (63.1) | 1108 (62.8) | 284 (64.3) | |
| Uncertain/missing | 22 (1.0) | 19 (1.1) | 3 (0.7) | |
| Year of transplant | .441 | |||
| 1996-2006 | 718 (32.5) | 581 (32.9) | 137 (31.0) | |
| 2007-2016 | 1489 (67.5) | 1184 (67.1) | 305 (69.0) | |
| Diagnosis | .652 | |||
| AML | 868 (39.3) | 703 (39.8) | 165 (37.3) | |
| ALL | 371 (16.8) | 296 (16.8) | 75 (17.0) | |
| ATL | 130 (5.9) | 102 (5.8) | 28 (6.3) | |
| CML | 124 (5.6) | 94 (5.3) | 30 (6.8) | |
| MDS | 342 (15.5) | 274 (15.5) | 68 (15.4) | |
| Other leukemia | 31 (1.4) | 23 (1.3) | 8 (1.8) | |
| MPN | 38 (1.7) | 28 (1.6) | 10 (2.3) | |
| NHL/HL/other lymphoma | 294 (13.3) | 236 (13.4) | 58 (13.1) | |
| MM/PCD | 9 (0.4) | 9 (0.5) | 0 (0.0) | |
| Follow-up of survivors | ||||
| Median time, month (range) | 52.5 (0.5-244.6) | 57.6 (0.5-244.6) | 58.6 (0.7-235.4) | .743 |
| Variable . | Total . | Training set . | Validation set . | P . |
|---|---|---|---|---|
| n = 2207 (%) . | n = 1765 (%) . | n = 442 (%) . | ||
| Age group at transplant, y | .327 | |||
| ≤30 | 339 (15.4) | 265 (15.0) | 74 (16.7) | |
| >30-40 | 340 (15.4) | 277 (15.7) | 63 (14.3) | |
| >40-50 | 480 (21.7) | 376 (21.3) | 104 (23.5) | |
| >50-60 | 631 (28.6) | 509 (28.8) | 122 (27.6) | |
| >60 | 417 (18.9) | 338 (19.2) | 79 (17.9) | |
| Sex | .572 | |||
| Male | 925 (41.9) | 734 (41.6) | 191 (43.2) | |
| Female | 1282 (58.1) | 1031 (58.4) | 251 (56.8) | |
| Source of stem cells | .279 | |||
| BM | 1349 (61.1) | 1061 (60.1) | 288 (65.2) | |
| Peripheral blood | 356 (16.1) | 292 (16.5) | 64 (14.5) | |
| BM + peripheral blood | 7 (0.3) | 6 (0.3) | 1 (0.2) | |
| Cord blood | 495 (22.4) | 406 (23.0) | 89 (20.1) | |
| Time from diagnosis to transplant | .707 | |||
| ≤6 mo | 793 (35.9) | 638 (36.1) | 155 (35.1) | |
| >6 mo | 1392 (63.1) | 1108 (62.8) | 284 (64.3) | |
| Uncertain/missing | 22 (1.0) | 19 (1.1) | 3 (0.7) | |
| Year of transplant | .441 | |||
| 1996-2006 | 718 (32.5) | 581 (32.9) | 137 (31.0) | |
| 2007-2016 | 1489 (67.5) | 1184 (67.1) | 305 (69.0) | |
| Diagnosis | .652 | |||
| AML | 868 (39.3) | 703 (39.8) | 165 (37.3) | |
| ALL | 371 (16.8) | 296 (16.8) | 75 (17.0) | |
| ATL | 130 (5.9) | 102 (5.8) | 28 (6.3) | |
| CML | 124 (5.6) | 94 (5.3) | 30 (6.8) | |
| MDS | 342 (15.5) | 274 (15.5) | 68 (15.4) | |
| Other leukemia | 31 (1.4) | 23 (1.3) | 8 (1.8) | |
| MPN | 38 (1.7) | 28 (1.6) | 10 (2.3) | |
| NHL/HL/other lymphoma | 294 (13.3) | 236 (13.4) | 58 (13.1) | |
| MM/PCD | 9 (0.4) | 9 (0.5) | 0 (0.0) | |
| Follow-up of survivors | ||||
| Median time, month (range) | 52.5 (0.5-244.6) | 57.6 (0.5-244.6) | 58.6 (0.7-235.4) | .743 |
ALL, acute lymphoblastic leukemia; AML, acute myeloid leukemia; CML, chronic myeloid leukemia; HL, Hodgkin lymphoma; MDS, myelodysplastic syndrome; MM, multiple myeloma; MPN, myeloproliferative neoplasm; NHL, non-Hodgkin lymphoma; PCD, plasma cell disease.
Cox model, Random Survival Forest, and Dynamic DeepHit can directly handle competing risks. ADABoost, XGBoost, Extra Tree Classifier, Bagging Classifier, and Gradient Boosting Classifier belong to the class of multi-output tree-based ensemble algorithms. To allow these models to handle competing risks, we use the First Hitting Time model, which assumes that the individual hazard function is a form-fixed stochastic process.32 We then use these multi-output tree-based algorithms to estimate the probability density function of the first hitting time. In particular, for each patient, the predicted value is a vector: , where is the longest observed time and the time unit used in our study is 30 days (duration from to ). Given an individual with the covariate , these models estimate with the estimated probability , where denotes the occurrence of the event of interest.
SHapley Additive exPlanations (SHAP) values were calculated for the stacked ensemble model. First proposed by Lundberg and Lee,33 SHAP is a united approach to explain the output of any machine-learning or deep-learning model. SHAP is based on Shapley values, a concept from game theory that measures the average contribution of a feature value to the prediction across all possible combinations (or coalitions) of other features. The pseudocode to calculate the SHAP value for feature X can be described as follows: (1) Get all subsets of features S that do not contain X. (2) Compute the effects of adding X to all those subsets on the predictions. (3) Average over all the contributions to compute the marginal contribution.
We used the Cox-PH model as the benchmark case and evaluated the models’ performance using inverse probability censoring weighted version of the C statistic (C-index) for single-risk models and the truncated C-index for competing-risk models.34,35 We used the restricted cubic splines approach to calculate the smoothed calibration curves and compute the integrated calibration index (ICI) and the median of the absolute difference between the predicted survival probabilities and smoothed survival frequencies (E50) to assess the calibration of different survival models.36 We first used the model to calculate the risk score for each patient in the validation set and get the median risk score. The high-risk group was defined as patients with a risk score above this median risk score whereas the low-risk group was defined as patients with a risk score below this median risk score. We also validated the final risk scores in the validation set using the Cox regression model or Fine-Gray competing risk model.
Other statistical considerations
Descriptive statistics were used to summarize patient characteristics. Comparisons of intergroup distributions were performed with the χ-square test or Fisher’s exact test for categorical variables and the Kruskal-Wallis test for continuous variables. The probability of GRFS and OS was estimated using the Kaplan-Meier method. Cumulative incidences for relapse, NRM, and GVHD were calculated using the cumulative incidence function to account for competing risks.37 Competing events were death without relapse for relapse, relapse for NRM, and death without GVHD for acute and chronic GVHD. P values < .05 were considered significant. All statistical analyses were performed with Python version 3.7 (Python Software Foundation, Fredricksburg, VA) and R version 3.6.1 (The R Foundation for Statistical Computing, Vienna, Austria).
Results
Patient characteristics
We included and evaluated 2207 adult patients who underwent their first allogeneic HSCT for hematologic malignancies (Table 1; supplemental Tables 1 and 2). The median follow-up period for survivors was 52.5 months (range 0.5-244.6) after HSCT. The most common indication of HSCT was acute myeloid leukemia (n = 868; 39.3%) followed by acute lymphoblastic leukemia (n = 371; 16.8%), myelodysplastic syndrome (n = 342; 15.5%), and mature lymphoid neoplasms (lymphoma/myeloma; n = 294; 13.3%). The graft source was mainly BM (61.1%) followed by cord blood (22.4%) and peripheral blood (16.1%). Frequency of patients transplanted with HLA 1 antigen-mismatched patients was higher in the validation cohort than in the training cohort (22.2% vs 15.8%; P = .011). There was no significant difference between the training cohort and the validation cohort other than the number of HLA antigen mismatches.
Comparison of predictive models
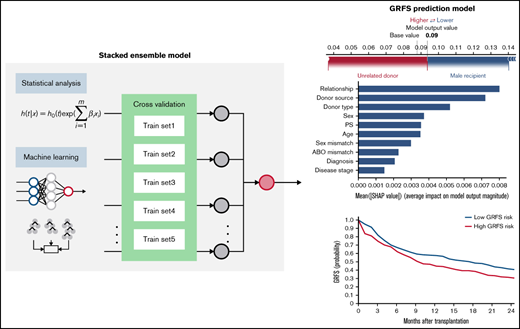
Prediction models were generated using a stacked ensemble containing 1 classical statistical analysis, 1 deep-learning model, and 6 machine-learning algorithms (Figure 1). The novel stacked ensemble model achieved a higher C-index for GRFS (C-index: 0.670) than other competing risk models in the validation dataset (Table 2; Cox-PH: 0.668; Random Survival Forest: 0.660; XGBoost: 0.602; Gradient Boosting: 0.630; Component-wise Gradient Boosting: 0.663; Dynamic DeepHit: 0.646). This model also showed the highest C-index for OS (C-index: 0.763), relapse (C-index: 0.793), NRM (C-index: 0.777), grade II-IV acute GVHD (C-index: 0.656), and chronic GVHD (C-index: 0.583). We also calculated C-index for patients who received transplant between 2007 and 2018 in validation dataset and confirmed that the stacked ensemble model showed the highest C-index (supplemental Table 3; GRFS: 0.844; OS: 0.716; relapse: 0.819; NRM: 0.770; grade II-IV acute GVHD: 0.536; chronic GVHD: 0.606). The stacked ensemble model showed the smallest ICI for GRFS (0.023), OS (0.210), relapse (0.044), grade II-IV acute GVHD (0.017), and chronic GVHD (0.258) and achieved the smallest E50 other than for GRFS and chronic GVHD, for which the stacked ensemble model showed the second smallest E50 (Table 3; supplemental Figure 1). Compared with other state-of-the-art competing risk models, the stacked ensemble model achieves higher C-index and smaller ICI for GRFS, OS, relapse, NRM, and GVHD, and we used this model for feature extraction and prediction.
Stacked ensemble model of machine-learning algorithms. Scheme of meta-model construction using stacking as an ensemble method.
Stacked ensemble model of machine-learning algorithms. Scheme of meta-model construction using stacking as an ensemble method.
Performance of each prediction model according to C-index in the validation cohort
| Risk category . | GRFS . | OS . | Relapse . | NRM . | aGVHD . | cGVHD . |
|---|---|---|---|---|---|---|
| Cox-PH | 0.668 | 0.740 | 0.770 | 0.664 | 0.651 | 0.564 |
| Fine-Gray competing risk model | NA | NA | 0.719 | 0.577 | 0.582 | 0.516 |
| Random Survival Forest | 0.660 | 0.745 | 0.788 | 0.761 | 0.580 | 0.577 |
| XGBoost | 0.602 | 0.712 | 0.756 | 0.543 | 0.540 | 0.573 |
| Gradient Boosting | 0.630 | 0.602 | 0.754 | 0.453 | 0.590 | 0.505 |
| Component-wise Gradient Boosting | 0.663 | 0.652 | 0.774 | 0.585 | 0.464 | 0.570 |
| Dynamic DeepHit | 0.646 | 0.710 | 0.730 | 0.691 | 0.537 | 0.555 |
| Stacked Ensemble Model | 0.670 | 0.763 | 0.793 | 0.777 | 0.656 | 0.583 |
| Risk category . | GRFS . | OS . | Relapse . | NRM . | aGVHD . | cGVHD . |
|---|---|---|---|---|---|---|
| Cox-PH | 0.668 | 0.740 | 0.770 | 0.664 | 0.651 | 0.564 |
| Fine-Gray competing risk model | NA | NA | 0.719 | 0.577 | 0.582 | 0.516 |
| Random Survival Forest | 0.660 | 0.745 | 0.788 | 0.761 | 0.580 | 0.577 |
| XGBoost | 0.602 | 0.712 | 0.756 | 0.543 | 0.540 | 0.573 |
| Gradient Boosting | 0.630 | 0.602 | 0.754 | 0.453 | 0.590 | 0.505 |
| Component-wise Gradient Boosting | 0.663 | 0.652 | 0.774 | 0.585 | 0.464 | 0.570 |
| Dynamic DeepHit | 0.646 | 0.710 | 0.730 | 0.691 | 0.537 | 0.555 |
| Stacked Ensemble Model | 0.670 | 0.763 | 0.793 | 0.777 | 0.656 | 0.583 |
aGVHD, grade II-IV acute GVHD; cGVHD, chronic GVHD; NA, not applicable.
Comparison of the Integrated Calibration Index and the median of the absolute difference between the predicted survival probabilities and smoothed survival frequencies for each prediction model
| . | Integrated calibration index (EC50) . | ||||
|---|---|---|---|---|---|
| Risk category . | GRFS . | OS . | Relapse . | aGVHD . | cGVHD . |
| Cox-PH | 0.139 (0.151) | 0.283 (0.248) | 0.055 (0.029) | 0.218 (0.212) | 0.263 (0.208) |
| Random Survival Forest | 0.142 (0.147) | 0.365 (0.372) | 0.048 (0.029) | 0.173 (0.178) | 0.345 (0.346) |
| XGBoost | 0.027 (0.007) | 0.393 (0.381) | 0.176 (0.163) | 0.265 (0.264) | 0.306 (0.265) |
| Gradient Boosting | 0.050 (0.047) | 0.438 (0.449) | 0.159 (0.129) | 0.254 (0.256) | 0.309 (0.275) |
| Component-wise Gradient Boosting | 0.061 (0.068) | 0.397 (0.395) | 0.171 (0.145) | 0.261 (0.264) | 0.324 (0.318) |
| Dynamic DeepHit | 0.054 (0.059) | 0.405 (0.409) | 0.152 (0.153) | 0.106 (0.108) | 0.319 (0.320) |
| Stacked Ensemble Model | 0.023 (0.017) | 0.210 (0.194) | 0.044 (0.018) | 0.017 (0.018) | 0.258 (0.226) |
| . | Integrated calibration index (EC50) . | ||||
|---|---|---|---|---|---|
| Risk category . | GRFS . | OS . | Relapse . | aGVHD . | cGVHD . |
| Cox-PH | 0.139 (0.151) | 0.283 (0.248) | 0.055 (0.029) | 0.218 (0.212) | 0.263 (0.208) |
| Random Survival Forest | 0.142 (0.147) | 0.365 (0.372) | 0.048 (0.029) | 0.173 (0.178) | 0.345 (0.346) |
| XGBoost | 0.027 (0.007) | 0.393 (0.381) | 0.176 (0.163) | 0.265 (0.264) | 0.306 (0.265) |
| Gradient Boosting | 0.050 (0.047) | 0.438 (0.449) | 0.159 (0.129) | 0.254 (0.256) | 0.309 (0.275) |
| Component-wise Gradient Boosting | 0.061 (0.068) | 0.397 (0.395) | 0.171 (0.145) | 0.261 (0.264) | 0.324 (0.318) |
| Dynamic DeepHit | 0.054 (0.059) | 0.405 (0.409) | 0.152 (0.153) | 0.106 (0.108) | 0.319 (0.320) |
| Stacked Ensemble Model | 0.023 (0.017) | 0.210 (0.194) | 0.044 (0.018) | 0.017 (0.018) | 0.258 (0.226) |
EC50, the median of the absolute difference between the predicted survival probabilities and smoothed survival frequencies.
Feature extraction and explanation
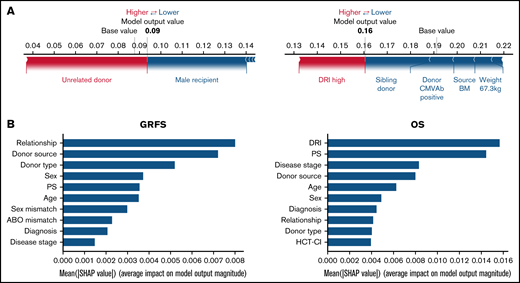
Using the stacked ensemble model, we calculated SHAP feature importance values for 26 variables that are used for model construction and ranked them according to their ability to discriminate between high- and low-risk patients. The SHAP value could explain the contribution of each variable to the estimate of GRFS for each patient (Figure 2A). Mean absolute value of the SHAP values for each variable could show the overall influence of each variable to model construction and their importance (Figure 2B). Characteristics about donors, including cell source, related donors or unrelated donors, and siblings or nonsibling relatives, were the most influential factors for GRFS. On the other hand, disease status before transplantation was the most influential factor for OS, as shown by high mean absolute SHAP value of DRI and disease stage.
SHapley Additive exPlanations feature importance value for GRFS and OS. (A) Representative patients in GRFS (left) and OS (right) model. Red and blue bars indicate positive and negative feature contributions, respectively. (B) SHAP feature importance measured as the mean absolute Shapley values for GRFS (left) and OS (right). Variables having top 10 highest impact on model outputs are shown.
SHapley Additive exPlanations feature importance value for GRFS and OS. (A) Representative patients in GRFS (left) and OS (right) model. Red and blue bars indicate positive and negative feature contributions, respectively. (B) SHAP feature importance measured as the mean absolute Shapley values for GRFS (left) and OS (right). Variables having top 10 highest impact on model outputs are shown.
Validation
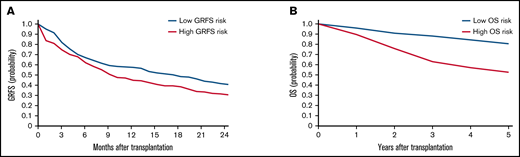
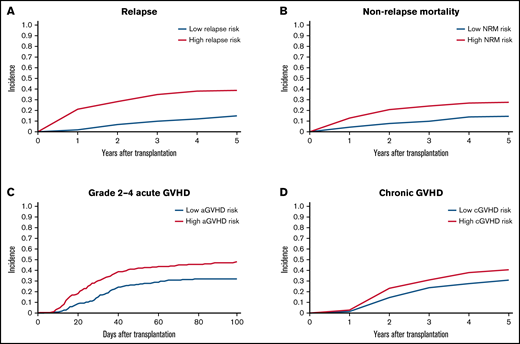
To validate the risk scores, we applied this model to the validation set. Based on the prediction score for each patient derived from the stacked ensemble model, we classified the final risk scores in the validation set into 2 groups: (1) high risk (above median) and (2) low risk (below median) for each of the risk categories. The probability of GRFS after 1 year and 2 years was 44.80% and 30.54% for the high-risk group and 57.47% and 40.69% for the low-risk group, respectively (Figure 3; hazard ratio [HR] compared with the low risk: 2.127; 95% CI, 1.19-3.80). The OS at 5 years was 52.58% for the high-risk group and 80.54% for the low-risk group (HR: 2.67; 95% CI, 2.02-3.52). Cumulative incidence of relapse at 5 years was 34.78% for the high-risk group and 13.61% for the low-risk group (Figure 4; HR compared with the low risk: 2.72; 95% CI, 1.85-3.99). The cumulative incidence of NRM at 5 years was 22.13% for the high-risk group and 12.92% for the low-risk group (HR compared with the low risk: 1.947; 95% CI, 1.24-2.74). The cumulative incidence of grade II-IV acute GVHD at 100 days was 46.61% for the high-risk group and 30.02% for the low-risk group (HR compared with the low risk: 1.66, 95% CI, 1.22-2.27). The cumulative incidence of chronic GVHD at 5 years was 35.20% for the high-risk group and 22.50% for the low-risk group (HR: 1.97; 95% CI, 1.44-2.70).
Kaplan-Meier estimates for GRFS and OS in the validation set. Estimates for GRFS (A) and OS (B) are shown. Patients are stratified based on stacked ensemble meta-model score.
Kaplan-Meier estimates for GRFS and OS in the validation set. Estimates for GRFS (A) and OS (B) are shown. Patients are stratified based on stacked ensemble meta-model score.
Cumulative incidence of relapse, NRM, and GVHD. (A) Relapse. (B) NRM. (C) Grade II-IV acute GVHD. (D) Chronic GVHD. Patients are stratified based on stacked ensemble meta-model score.
Cumulative incidence of relapse, NRM, and GVHD. (A) Relapse. (B) NRM. (C) Grade II-IV acute GVHD. (D) Chronic GVHD. Patients are stratified based on stacked ensemble meta-model score.
Discussion
We successfully developed a novel prediction model for GRFS using the stacked ensemble of classical statistical analysis and multiple machine-learning algorithms. This study showed for the first time the improvement of predictive accuracy for GRFS using ensemble learning applicable for right-censored medical record data.
Our ensemble model is designed to handle right-censored data, a form of missing data problem specific for survival analysis. As a result, its outputs can be directly compared with classical algorithms such as Cox-PH or Fine-Gray model. Ignoring censored patients could potentially give a bias to the outcome. The longer the follow-up time, the larger this bias due to an increasing number of censored patients. Shouval et al13 used Random Survival Forest to analyze right-censored data and successfully established an umbilical cord blood transplantation risk score that could predict OS and RFS at 2 years in patients with acute leukemia who received cord blood transplantation. In addition, our model can analyze data with multiple competing risks and can be modified to include time-varying variables. Finally, by combining the outputs of various machine-learning methods, our ensemble model outperforms not only classical algorithms but also the most cutting-edge machine-learning models for survival analysis.
Stacking is an ensemble method that combines multiple heterogenous algorithms into single better predictive model. Sachs et al developed a stacking method with a pseudo-observation approach for ensemble of various machine-learning algorithms handling right-censored data.38 A diverse set of initial classifiers is the fundamental aspect for establishing an accurate ensemble model, so our ensemble model used 8 algorithms, including statistical analysis and tree-based and neural-network–based learning for meta-model construction.
One of the fundamental advantages of the machine-learning–based data mining approach is unbiased feature selection and prediction; on the other hand, its hidden nature of model construction and prediction makes it difficult for us to interpret the contribution of variables toward end points.9 Although this novel ensemble method provides superior prediction to conventional statistical analysis and each machine-learning algorithm, stacked-ensemble lost the interpretable tree-like structure of decision tree–based learning. Therefore, we introduced SHAP value for explanation of model prediction. In addition to the influence of each variable on model construction, SHAP value could extract and clearly visualize the contribution of each variable for personalized prediction of individual patients.
In addition to the hidden nature of model construction, the criteria for selection of machine-learning algorithms were often unclarified. A previous report using Japanese Transplant Unified Management Program created a prediction model derived from alternating decision tree based on its highest value of area under the curve.11 Our ensemble model showed higher C-index value than Cox-PH or state-of-the-art machine-learning algorithms for GRFS and OS. Validated by these findings, we used the stacked ensemble meta-model for further analysis.
GRFS was initially developed by Holtan et al to incorporate 2 major posttransplantation complications, relapse and GVHD, into a single end point.15 GRFS is useful for understanding ongoing morbidity due to GVHD that could not be interpreted by OS or RFS. For example, previous studies found that BM donors showed higher GRFS than peripheral blood stem cell donors in matched-sibling donors although BM and peripheral blood stem cell did not show difference in terms of OS or RFS. However, composite end points using right-censored data only measure the time to the first event, and GRFS cannot replace OS, RFS, or GVHD. Magenau et al reported that chronic GVHD had less modulating effect on OS than grade III-IV acute GVHD or relapse.39 This is partly explained by the association of graft-versus-leukemia effect with chronic GVHD.40 On the other hand, chronic GVHD has tremendous negative impact on quality of daily life after transplantation even under mild to moderate symptoms.41 To understand the efficacy of the stacked ensemble model on different end points after transplantation, we also analyzed OS, relapse, NRM, grade II-IV GVHD, and chronic GVHD, respectively. For all end points, the stacked ensemble model showed better predictive accuracy than other models, which validated the versatility and robustness of this model.
Several study limitations should be noted. One of the limitations is that this model is not completely free from hypothesis in terms of feature selection. We used 26 variables accessible in the registry for establishment of prediction models but might still ignore unknown or unavailable risk factors. For example, center effect was reported to be associated with HSCT outcome, but existence of unknown factors was suggested.42 Okamura et al14 developed a web application tool for OS, progression-free survival, relapse, and NRM after HSCT in a single center and provided their source code for in-house prognosis prediction using random survival forest. A center-specific prediction model might be able to overcome institution-associated bias, but standardization of prediction algorithms is still required. In addition to limited number of variables, some of the variables were categorized into subgroups based on clinically established criteria. For example, although HLA mismatch is categorized based on the number of mismatched antigens or alleles, each mismatch causes different immunological interaction between donor cells and recipient cells.21,43-46 Because we categorized patients into 6 groups according to the number of mismatched antigens or alleles, we could not consider their mismatched locus. Another example is DRI. We stratified pretransplant disease condition using DRI or disease status, which does not reflect recent progress in clinical implementation of genome sequencing technology.47,48 Nazha et al established prediction model that could integrate clinical and mutational variables into a single model using Random Survival Forest.49 Gandelman et al successfully stratified chronic GVHD severity using computational workflow made of visualization of high-dimensional single-cell data based on the t-Distributed Stochastic Neighbor Embedding algorithm, self-organizing maps, and marker enrichment modeling.50 Wider range of data collection and categorization of variables using machine learning–based clustering methods might contribute to unbiased variable selection and calculation.
Sample size also limited risk stratification of our model. In this study, we used C-index for evaluation and comparison of the predictive accuracy of prediction models, and the novel meta-model showed highest value for C-index. However, due to the small size of the validation set, we only classified the final risk scores into 2 groups. Moreover, these findings should be interpreted carefully from the viewpoint of bias in this registry data derived from known and unknown factors. Our dataset did not include the information about posttransplant cyclophosphamide usage, especially in haploidentical HSCT, maintenance therapy, and prophylaxis for fungal or viral infection. Other unknown factors, including center effect and different distribution of HLA alleles and haplotypes, might be influential in transplant outcomes. Further validation of the stacked ensemble model using different registry data is warranted.
In conclusion, we improved machine-learning predictive accuracy of GRFS using a stacked ensemble meta-model feasible for right-censored medical record data. This model provides direct and versatile application of machine-learning algorithms for time-to-event analysis. A user-friendly Web tool for personalized pretransplant prediction of HSCT outcome is now being constructed. Although external validation using larger data with more detailed patient information is required for individualized prediction and treatment, this ensemble-learning model will be useful for risk stratification of morbidity and mortality after HSCT from pretransplant characteristics.
Acknowledgments
The authors are grateful to Emi Furusaka, Miki Shirasu, Tomoko Okuda, and Megumi Oka for their expert data management and secretarial assistance and all members of the transplant centers in KSCTG for their dedicated care of patients and donors.
This work was supported by grants from AMED (JP18pc0101031), JSPS KAKENHI (18K08325), and Takeda Science Foundation (J.K.).
Authorship
Contribution: J.K., I.M., and M.M. designed the study; M. Iwasaki, J.K., I.M., and L.M.A. conducted the study and drafted the manuscript; I.M. and L.M.A. analyzed the data; Y.A., T. Kondo, T.I., Y.U., K.I., T.A., A.Y., K.Y., M.N., N. Anzai, T.M., T. Kitano, M. Itoh, N. Arima, T.T., M.W., H.H., K.A., and A.T.-K. contributed to the data collection and the final draft of the study; and all authors read and approved the final manuscript.
Conflict-of-interest disclosure: J.K. received honoraria from Takeda Phamaceutical, Celgene, Novartis Pharma, Astellas Pharma, Chugai Pharmaceutical, Kyowa Kirin, Otsuka Pharmaceutical, Bristol Myers Squibb, JCR Pharmaceuticals, MSD, and Daiichi Sankyo outside the submitted work. J.K. has a patent blood disease prognosis prediction information generation system, information processing device, server, program, or method (patent number: JP2020-119383) pending to NextGeM Inc., Kyoto University. T. Kondo reported grants and honoraria from Asahi Kasei Pharma and honoraria from Otsuka Pharmaceutical, Sumitomo Dainippon Pharma, Astellas Pharma, MSD Pharma, Pfizer, Kyowa Kirin, and Chugai Pharmaceutical outside the submitted work. T.I. reported a grant from Ono Pharmaceutical outside the submitted work. K.I. reported honoraria from Ono Pharmaceutical, Celgene, Bristol Myers Squibb, Takeda Pharmaceutical, Novartis Pharma, Nippon Shinyaku, Chugai Pharmaceutical, Kyowa Kirin, Otsuka Pharmaceutical, and Astellas Pharma outside the submitted work. T. Kitano reported grants and honoraria from Kyowa Kirin, Chugai Pharmaceutical, and Eizai, grants from Teijin Pharma, and honoraria from Bristol Myers Squibb, Celgene, and Ono Pharmaceutical outside the submitted work. I.M., L.M.A., and M.M. have a patent blood disease prognosis prediction information generation system, information processing device, server, program, or method (patent number: JP2020-119383) pending to NextGeM Inc., Kyoto University. A.T.-K. reported grants and honoraria from Celgene, Bristol Myers Squibb, Asteras Pharma, and Kyowa Kirin, grants from Ono Pharmaceutical, Thyas, Takeda Pharmaceutical, Chugai Pharmaceutical, Eizai, Nippon Shinyaku, Otsuka Pharmaceutical, Pfizer, Ohara Pharmaceutical, and Sanofi, and honoraria from Novartis Pharma, and MSD outside the submitted work. The remaining authors declare no competing financial interests.
A full list of study group members appears in “ Appendix.”
Correspondence: Junya Kanda, Department of Hematology and Oncology, Graduate School of Medicine, Kyoto University, 54 Kawaharacho, Shogoin, Sakyo-ku, Kyoto, Japan, 606-8507; e-mail: jkanda16@kuhp.kyoto-u.ac.jp.
Appendix: study group members
Investigators of the Kyoto Stem Cell Transplantation Group have 2 different statuses: authors and collaborators. Authors: Makoto Iwasaki, Junya Kanda, Yasuyuki Arai, Tadakazu Kondo, Takayuki Ishikawa, Yasunori Ueda, Kazunori Imada, Takashi Akasaka, Akihito Yonezawa, Kazuhiro Yago, Masaharu Nohgawa, Naoyuki Anzai, Toshinori Moriguchi, Toshiyuki Kitano, Mitsuru Itoh, Nobuyoshi Arima, Tomoharu Takeoka, Mitsumasa Watanabe, Hirokazu Hirata, Kosuke Asagoe, and Akifumi Takaori-Kondo. Collaborators: Masakatsu Hishizawa, Rie Tabata, Takashi Ikeda, Yoshitomo Maesako, Noboru Yonetani, Satoshi Oka, Satoshi Yoshioka, Nobuhiro Hiramoto, Fumiya Wada, Yutaka Shimazu, Chisaki Mizumoto, Yusuke Tashiro, Naoki Tamura, Takuto Mori, Tomohiro Taya, Tomoki Iemura, Hiroyuki Matsui, Yoshinobu Konishi, Kiyotaka Izumi, Hiroyuki Muranushi, Mizuki Watanabe, Suguru Takeuchi, Kensuke Nakao, and Mari Morita-Fujita.
References
Author notes
Requests for data sharing may be submitted to Junya Kanda (jkanda16@kuhp.kyoto-u.ac.jp).
The full-text version of this article contains a data supplement.